Предел функции в картинках (определения, свойства и теоремы)

Приводятся определения, свойства и теоремы пределов функций в сжатом виде. Каждая картинка содержит основные формулы и понятия страницы, на которую указывает ссылка, связанная с заголовком.
Здесь приводится оглавление раздела «Предел функции» в виде главных изображений страниц, входящих в этот раздел. На этих изображениях, в кратком виде представлены главные содержания страниц раздела. На многих из них даются свойства и теоремы, относящиеся к пределам функций. Снизу от каждого изображения имеется заголовок и ссылка на страницу, к которой относится картинка. Просматривая их, можно освежить в памяти определения, свойства и теоремы пределов функций.
Предел функции – определения, теоремы и свойства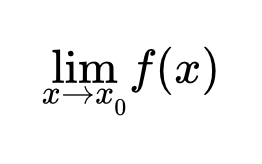 Приводятся формулировки основных теорем и свойств предела функции. Даны определения конечных и бесконечных пределов в конечных точках и на бесконечности (двусторонних и односторонних) по Коши и Гейне. Рассмотрены арифметические свойства; теоремы, связанные с неравенствами; критерий сходимости Коши; предел сложной функции; свойства бесконечно малых, бесконечно больших и монотонных функций. Дано определение функции. Определение функции
Приводятся формулировки основных теорем и свойств предела функции. Даны определения конечных и бесконечных пределов в конечных точках и на бесконечности (двусторонних и односторонних) по Коши и Гейне. Рассмотрены арифметические свойства; теоремы, связанные с неравенствами; критерий сходимости Коши; предел сложной функции; свойства бесконечно малых, бесконечно больших и монотонных функций. Дано определение функции. Определение функции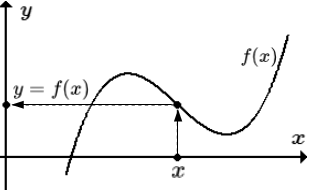 Определение функции, области задания и множества значений. Определения, связанные с обозначением функции. Определения сложной, числовой, действительной, монотонной и многозначной функции. Определения максимума, минимума, верхней и нижней граней для ограниченных функций. Сужение и продолжение функций.
Определение функции, области задания и множества значений. Определения, связанные с обозначением функции. Определения сложной, числовой, действительной, монотонной и многозначной функции. Определения максимума, минимума, верхней и нижней граней для ограниченных функций. Сужение и продолжение функций. 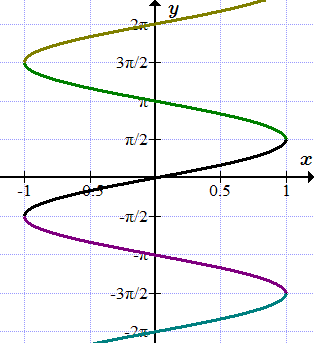 Пример многозначной функции. Различными цветами обозначены ее ветви. Каждая ветвь является функцией. Способы задания функций
Пример многозначной функции. Различными цветами обозначены ее ветви. Каждая ветвь является функцией. Способы задания функций Приводятся основные способы задания функций: явный аналитический; интервальный; параметрический; неявный; задание функции с помощью ряда; табличный; графический. Примеры применения этих способов Окрестность точки
Приводятся основные способы задания функций: явный аналитический; интервальный; параметрический; неявный; задание функции с помощью ряда; табличный; графический. Примеры применения этих способов Окрестность точки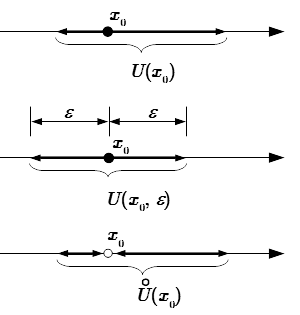 Рассмотрено общее определение окрестности точки на числовой прямой. Определения эпсилон окрестности, левосторонней, правосторонней и проколотых окрестностей конечных и бесконечно удаленных точек. Свойство окрестности. Доказана теорема о равносильности использования эпсилон окрестности и произвольной окрестности в определении предела функции по Коши. Универсальное определение предела функции по Гейне и по Коши
Рассмотрено общее определение окрестности точки на числовой прямой. Определения эпсилон окрестности, левосторонней, правосторонней и проколотых окрестностей конечных и бесконечно удаленных точек. Свойство окрестности. Доказана теорема о равносильности использования эпсилон окрестности и произвольной окрестности в определении предела функции по Коши. Универсальное определение предела функции по Гейне и по Коши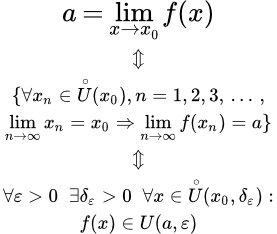 Приводятся определения предела функции по Гейне (через последовательности) и по Коши (через эпсилон и дельта окрестности). Определения даются в универсальном виде, применимом как для двусторонних, так и односторонних пределов в конечных и бесконечно удаленных точках. Рассмотрено определение, что точка a не является пределом функции. Доказательство эквивалентности определений по Гейне и по Коши.
Приводятся определения предела функции по Гейне (через последовательности) и по Коши (через эпсилон и дельта окрестности). Определения даются в универсальном виде, применимом как для двусторонних, так и односторонних пределов в конечных и бесконечно удаленных точках. Рассмотрено определение, что точка a не является пределом функции. Доказательство эквивалентности определений по Гейне и по Коши. 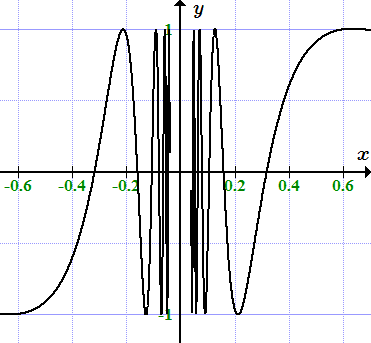 Функция f(x) = sin(1/x) не имеет предела при x → 0. Определение предела функции в конечной точке
Функция f(x) = sin(1/x) не имеет предела при x → 0. Определение предела функции в конечной точке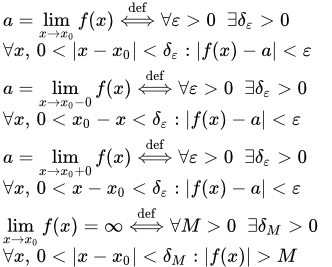 Даны определения пределов функции в конечной точке по Коши. Рассмотрены определения двусторонних и односторонних пределов (слева и справа). Также приводятся определения бесконечных пределов в конечной точке. Разобраны примеры решений задач, в которых требуется показать, что предел равен заданному значению, используя определение Коши.
Даны определения пределов функции в конечной точке по Коши. Рассмотрены определения двусторонних и односторонних пределов (слева и справа). Также приводятся определения бесконечных пределов в конечной точке. Разобраны примеры решений задач, в которых требуется показать, что предел равен заданному значению, используя определение Коши. 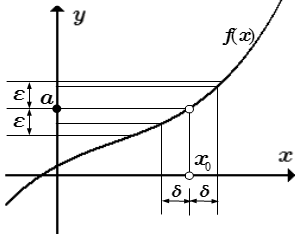 Предел функции в точке:
Предел функции в точке:
|f(x) – a| < ε при 0 < |x – x0| < δ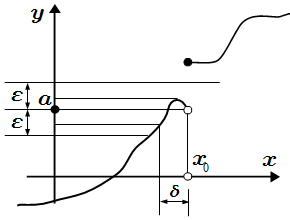 Левый предел функции в точке:
Левый предел функции в точке:
|f(x) – a| < ε при 0 < x0 – x < δ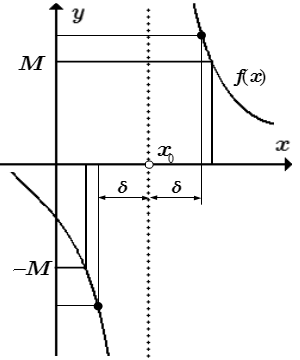 Бесконечный предел функции в точке:
Бесконечный предел функции в точке:
|f(x)| > M при 0 < |x – x0| < δ Определение предела функции на бесконечности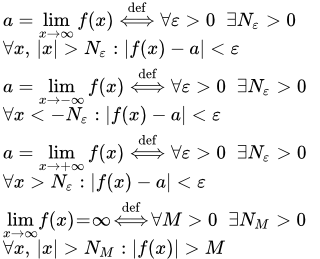 Определения конечных и бесконечных пределов функции на бесконечности по Коши. Определения двусторонних и односторонних пределов (слева и справа). Примеры решений задач, в которых, используя определение Коши, требуется показать, что предел на бесконечности равен заданному значению, .
Определения конечных и бесконечных пределов функции на бесконечности по Коши. Определения двусторонних и односторонних пределов (слева и справа). Примеры решений задач, в которых, используя определение Коши, требуется показать, что предел на бесконечности равен заданному значению, . 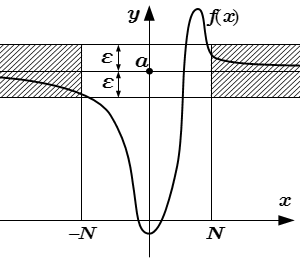 Предел функции на бесконечности:
Предел функции на бесконечности:
|f(x) – a| < ε при |x| > N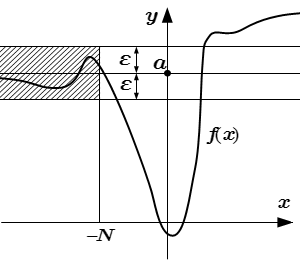 Левый предел функции на бесконечности:
Левый предел функции на бесконечности:
|f(x) – a| < ε при x < –N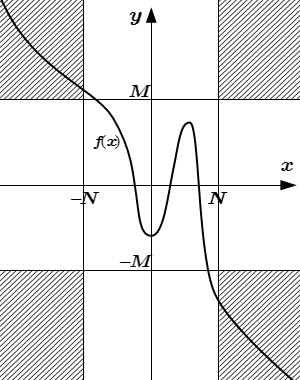 Бесконечный предел функции на бесконечности:
Бесконечный предел функции на бесконечности:
|f(x)| > M при |x| > N Основные свойства предела функции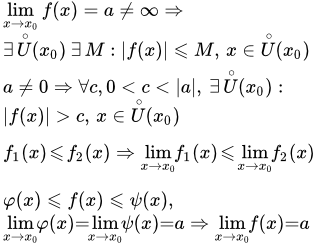 Приводятся доказательства основных теорем и свойств предела функции: о влиянии значений функции в конечном числе точек на величину предела; теоремы об ограниченности функции; предел постоянной; свойства, связанные с неравенствами. Теорема о пределе промежуточной функции
Приводятся доказательства основных теорем и свойств предела функции: о влиянии значений функции в конечном числе точек на величину предела; теоремы об ограниченности функции; предел постоянной; свойства, связанные с неравенствами. Теорема о пределе промежуточной функции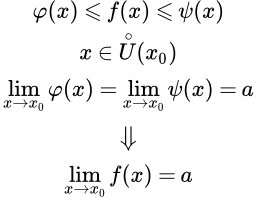 Приводится формулировка и доказательство теоремы о пределе промежуточной (зажатой) функции. Доказательство основывается на аналогичной теореме для последовательностей. Арифметические свойства предела функции
Приводится формулировка и доказательство теоремы о пределе промежуточной (зажатой) функции. Доказательство основывается на аналогичной теореме для последовательностей. Арифметические свойства предела функции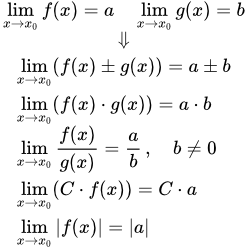 Приводятся доказательства арифметических свойств пределов функций: предел от суммы, разности, произведения и частного двух функций. Произведено обобщение на конечное число функций. Рассмотрен пример применения арифметических свойств. Критерий Коши существования предела функции
Приводятся доказательства арифметических свойств пределов функций: предел от суммы, разности, произведения и частного двух функций. Произведено обобщение на конечное число функций. Рассмотрен пример применения арифметических свойств. Критерий Коши существования предела функции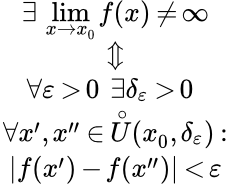 Определение условия Коши для функции. Формулировка и доказательство критерия Коши существования предела функции. Бесконечно малые и бесконечно большие функции
Определение условия Коши для функции. Формулировка и доказательство критерия Коши существования предела функции. Бесконечно малые и бесконечно большие функции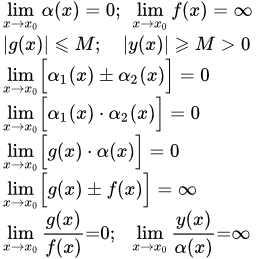 Определения и свойства бесконечно малых и бесконечно больших функций в точке. Связь между ними. Доказательства свойств и теорем. Арифметические свойства пределов с бесконечно малыми и бесконечно большими функциями. Пределы монотонных функций
Определения и свойства бесконечно малых и бесконечно больших функций в точке. Связь между ними. Доказательства свойств и теорем. Арифметические свойства пределов с бесконечно малыми и бесконечно большими функциями. Пределы монотонных функций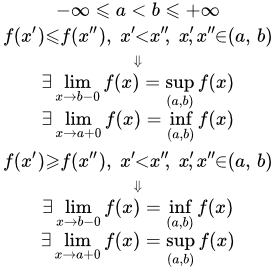 Теорема о пределе монотонной функции. Приводится доказательство теоремы, используя два метода. Также даны определения строго возрастающей, неубывающей, строго убывающей и невозрастающей функций. Определение монотонной функции. Теорема о пределе сложной функции
Теорема о пределе монотонной функции. Приводится доказательство теоремы, используя два метода. Также даны определения строго возрастающей, неубывающей, строго убывающей и невозрастающей функций. Определение монотонной функции. Теорема о пределе сложной функции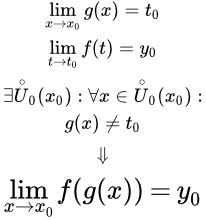 Приводится теорема о пределе сложной функции, и ее доказательство. Дана теорема, когда одна из функций, входящей в состав сложной функции, является монотонной. Рассмотрен пример определения предела в точке, в которой составная функция не является непрерывной.
Приводится теорема о пределе сложной функции, и ее доказательство. Дана теорема, когда одна из функций, входящей в состав сложной функции, является монотонной. Рассмотрен пример определения предела в точке, в которой составная функция не является непрерывной.
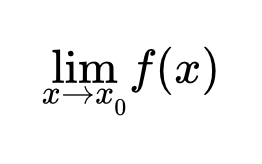 Приводятся формулировки основных теорем и свойств предела функции. Даны определения конечных и бесконечных пределов в конечных точках и на бесконечности (двусторонних и односторонних) по Коши и Гейне. Рассмотрены арифметические свойства; теоремы, связанные с неравенствами; критерий сходимости Коши; предел сложной функции; свойства бесконечно малых, бесконечно больших и монотонных функций. Дано определение функции. Определение функции
Приводятся формулировки основных теорем и свойств предела функции. Даны определения конечных и бесконечных пределов в конечных точках и на бесконечности (двусторонних и односторонних) по Коши и Гейне. Рассмотрены арифметические свойства; теоремы, связанные с неравенствами; критерий сходимости Коши; предел сложной функции; свойства бесконечно малых, бесконечно больших и монотонных функций. Дано определение функции. Определение функции Определение функции, области задания и множества значений. Определения, связанные с обозначением функции. Определения сложной, числовой, действительной, монотонной и многозначной функции. Определения максимума, минимума, верхней и нижней граней для ограниченных функций. Сужение и продолжение функций.
Определение функции, области задания и множества значений. Определения, связанные с обозначением функции. Определения сложной, числовой, действительной, монотонной и многозначной функции. Определения максимума, минимума, верхней и нижней граней для ограниченных функций. Сужение и продолжение функций. 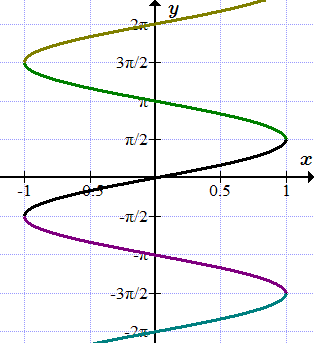 Пример многозначной функции. Различными цветами обозначены ее ветви. Каждая ветвь является функцией. Способы задания функций
Пример многозначной функции. Различными цветами обозначены ее ветви. Каждая ветвь является функцией. Способы задания функций Приводятся основные способы задания функций: явный аналитический; интервальный; параметрический; неявный; задание функции с помощью ряда; табличный; графический. Примеры применения этих способов Окрестность точки
Приводятся основные способы задания функций: явный аналитический; интервальный; параметрический; неявный; задание функции с помощью ряда; табличный; графический. Примеры применения этих способов Окрестность точки Рассмотрено общее определение окрестности точки на числовой прямой. Определения эпсилон окрестности, левосторонней, правосторонней и проколотых окрестностей конечных и бесконечно удаленных точек. Свойство окрестности. Доказана теорема о равносильности использования эпсилон окрестности и произвольной окрестности в определении предела функции по Коши. Универсальное определение предела функции по Гейне и по Коши
Рассмотрено общее определение окрестности точки на числовой прямой. Определения эпсилон окрестности, левосторонней, правосторонней и проколотых окрестностей конечных и бесконечно удаленных точек. Свойство окрестности. Доказана теорема о равносильности использования эпсилон окрестности и произвольной окрестности в определении предела функции по Коши. Универсальное определение предела функции по Гейне и по Коши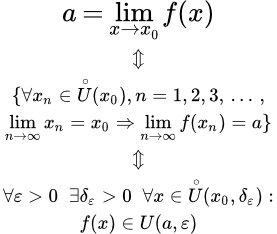 Приводятся определения предела функции по Гейне (через последовательности) и по Коши (через эпсилон и дельта окрестности). Определения даются в универсальном виде, применимом как для двусторонних, так и односторонних пределов в конечных и бесконечно удаленных точках. Рассмотрено определение, что точка a не является пределом функции. Доказательство эквивалентности определений по Гейне и по Коши.
Приводятся определения предела функции по Гейне (через последовательности) и по Коши (через эпсилон и дельта окрестности). Определения даются в универсальном виде, применимом как для двусторонних, так и односторонних пределов в конечных и бесконечно удаленных точках. Рассмотрено определение, что точка a не является пределом функции. Доказательство эквивалентности определений по Гейне и по Коши.  Функция f(x) = sin(1/x) не имеет предела при x → 0. Определение предела функции в конечной точке
Функция f(x) = sin(1/x) не имеет предела при x → 0. Определение предела функции в конечной точке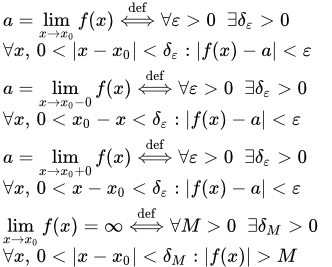 Даны определения пределов функции в конечной точке по Коши. Рассмотрены определения двусторонних и односторонних пределов (слева и справа). Также приводятся определения бесконечных пределов в конечной точке. Разобраны примеры решений задач, в которых требуется показать, что предел равен заданному значению, используя определение Коши.
Даны определения пределов функции в конечной точке по Коши. Рассмотрены определения двусторонних и односторонних пределов (слева и справа). Также приводятся определения бесконечных пределов в конечной точке. Разобраны примеры решений задач, в которых требуется показать, что предел равен заданному значению, используя определение Коши.  Предел функции в точке:
Предел функции в точке:|f(x) – a| < ε при 0 < |x – x0| < δ
 Левый предел функции в точке:
Левый предел функции в точке:|f(x) – a| < ε при 0 < x0 – x < δ
 Бесконечный предел функции в точке:
Бесконечный предел функции в точке:|f(x)| > M при 0 < |x – x0| < δ Определение предела функции на бесконечности
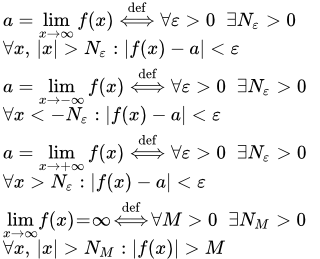 Определения конечных и бесконечных пределов функции на бесконечности по Коши. Определения двусторонних и односторонних пределов (слева и справа). Примеры решений задач, в которых, используя определение Коши, требуется показать, что предел на бесконечности равен заданному значению, .
Определения конечных и бесконечных пределов функции на бесконечности по Коши. Определения двусторонних и односторонних пределов (слева и справа). Примеры решений задач, в которых, используя определение Коши, требуется показать, что предел на бесконечности равен заданному значению, .  Предел функции на бесконечности:
Предел функции на бесконечности:|f(x) – a| < ε при |x| > N
 Левый предел функции на бесконечности:
Левый предел функции на бесконечности:|f(x) – a| < ε при x < –N
 Бесконечный предел функции на бесконечности:
Бесконечный предел функции на бесконечности:|f(x)| > M при |x| > N Основные свойства предела функции
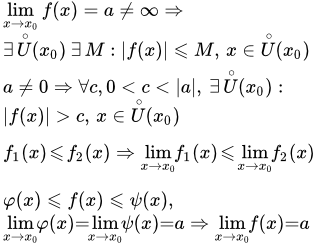 Приводятся доказательства основных теорем и свойств предела функции: о влиянии значений функции в конечном числе точек на величину предела; теоремы об ограниченности функции; предел постоянной; свойства, связанные с неравенствами. Теорема о пределе промежуточной функции
Приводятся доказательства основных теорем и свойств предела функции: о влиянии значений функции в конечном числе точек на величину предела; теоремы об ограниченности функции; предел постоянной; свойства, связанные с неравенствами. Теорема о пределе промежуточной функции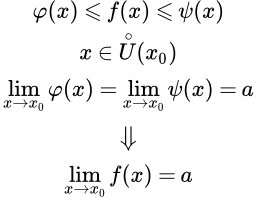 Приводится формулировка и доказательство теоремы о пределе промежуточной (зажатой) функции. Доказательство основывается на аналогичной теореме для последовательностей. Арифметические свойства предела функции
Приводится формулировка и доказательство теоремы о пределе промежуточной (зажатой) функции. Доказательство основывается на аналогичной теореме для последовательностей. Арифметические свойства предела функции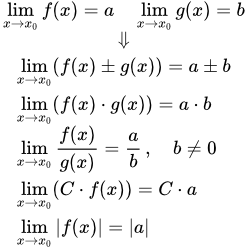 Приводятся доказательства арифметических свойств пределов функций: предел от суммы, разности, произведения и частного двух функций. Произведено обобщение на конечное число функций. Рассмотрен пример применения арифметических свойств. Критерий Коши существования предела функции
Приводятся доказательства арифметических свойств пределов функций: предел от суммы, разности, произведения и частного двух функций. Произведено обобщение на конечное число функций. Рассмотрен пример применения арифметических свойств. Критерий Коши существования предела функции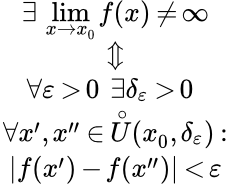 Определение условия Коши для функции. Формулировка и доказательство критерия Коши существования предела функции. Бесконечно малые и бесконечно большие функции
Определение условия Коши для функции. Формулировка и доказательство критерия Коши существования предела функции. Бесконечно малые и бесконечно большие функции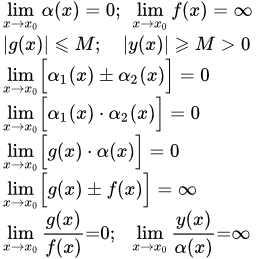 Определения и свойства бесконечно малых и бесконечно больших функций в точке. Связь между ними. Доказательства свойств и теорем. Арифметические свойства пределов с бесконечно малыми и бесконечно большими функциями. Пределы монотонных функций
Определения и свойства бесконечно малых и бесконечно больших функций в точке. Связь между ними. Доказательства свойств и теорем. Арифметические свойства пределов с бесконечно малыми и бесконечно большими функциями. Пределы монотонных функций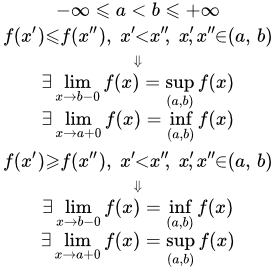 Теорема о пределе монотонной функции. Приводится доказательство теоремы, используя два метода. Также даны определения строго возрастающей, неубывающей, строго убывающей и невозрастающей функций. Определение монотонной функции. Теорема о пределе сложной функции
Теорема о пределе монотонной функции. Приводится доказательство теоремы, используя два метода. Также даны определения строго возрастающей, неубывающей, строго убывающей и невозрастающей функций. Определение монотонной функции. Теорема о пределе сложной функции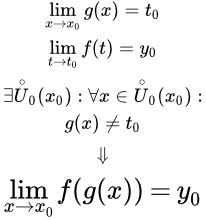 Приводится теорема о пределе сложной функции, и ее доказательство. Дана теорема, когда одна из функций, входящей в состав сложной функции, является монотонной. Рассмотрен пример определения предела в точке, в которой составная функция не является непрерывной.
Приводится теорема о пределе сложной функции, и ее доказательство. Дана теорема, когда одна из функций, входящей в состав сложной функции, является монотонной. Рассмотрен пример определения предела в точке, в которой составная функция не является непрерывной. 