Предел последовательности (свойства и теоремы в картинках)
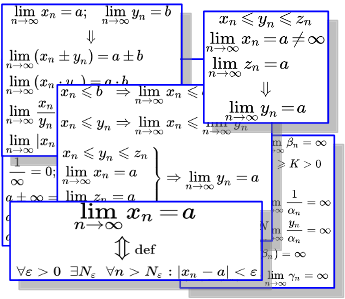
Приводятся основные свойства и теоремы пределов последовательностей в сжатом виде – в виде изображений. Каждая картинка снабжена заголовком и ссылкой на страницу с подробным изложением теории.
Здесь приводятся главные картинки раздела «Предел последовательности». На этих изображениях, в кратком виде представлены главные содержания страниц раздела. На многих из них даются свойства и теоремы, относящиеся к пределам последовательностей. Снизу от каждого изображения имеется заголовок и ссылка на страницу, к которой относится картинка. Просматривая эти картинки, можно освежить в памяти основные свойства и теоремы.
Предел последовательности – основные теоремы и свойства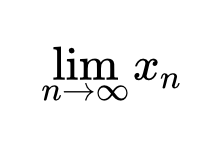 Приводятся формулировки основных теорем и свойств числовых последовательностей, имеющих предел. Содержится определение последовательности и ее предела. Рассмотрены арифметические действия с последовательностями, свойства, связанные с неравенствами, критерии сходимости, свойства бесконечно малых и бесконечно больших последовательностей. Определение числовой последовательности
Приводятся формулировки основных теорем и свойств числовых последовательностей, имеющих предел. Содержится определение последовательности и ее предела. Рассмотрены арифметические действия с последовательностями, свойства, связанные с неравенствами, критерии сходимости, свойства бесконечно малых и бесконечно больших последовательностей. Определение числовой последовательности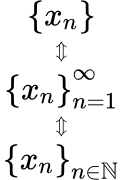 Приводится определение числовой последовательности. Рассмотрены примеры неограниченно возрастающих, сходящихся и расходящихся последовательностей. Рассмотрена последовательность, содержащая все рациональные числа.
Приводится определение числовой последовательности. Рассмотрены примеры неограниченно возрастающих, сходящихся и расходящихся последовательностей. Рассмотрена последовательность, содержащая все рациональные числа. 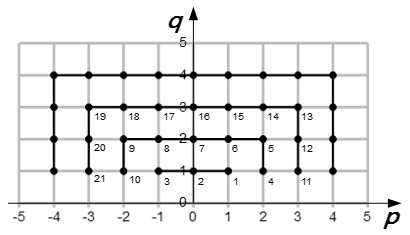 Способ нумерации рациональных чисел Определение конечного предела последовательности
Способ нумерации рациональных чисел Определение конечного предела последовательности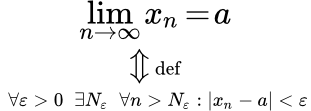 Приводится определение конечного предела последовательности. Рассмотрены связанные с этим свойства и эквивалентное определение. Приводится определение, что точка a не является пределом последовательности. Рассмотрены примеры, в которых доказывается существование предела, используя определение. Основные свойства конечных пределов последовательностей
Приводится определение конечного предела последовательности. Рассмотрены связанные с этим свойства и эквивалентное определение. Приводится определение, что точка a не является пределом последовательности. Рассмотрены примеры, в которых доказывается существование предела, используя определение. Основные свойства конечных пределов последовательностей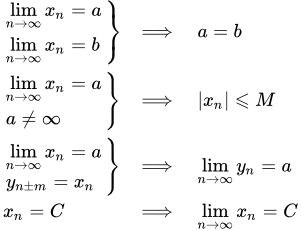 Приводятся формулировки и доказательства основных свойств числовых последовательностей, имеющих конечный предел. Среди них: теорема единственности предела, ограниченность сходящейся последовательности, влияние конечного числа элементов на сходимость. Арифметические свойства конечных пределов последовательностей
Приводятся формулировки и доказательства основных свойств числовых последовательностей, имеющих конечный предел. Среди них: теорема единственности предела, ограниченность сходящейся последовательности, влияние конечного числа элементов на сходимость. Арифметические свойства конечных пределов последовательностей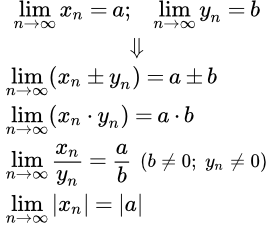 Приводятся формулировки и доказательства арифметических свойств последовательностей, имеющих конечный предел. Сюда входят предел суммы, разности, произведения и частного числовых последовательностей. Свойства пределов последовательностей, связанных неравенствами
Приводятся формулировки и доказательства арифметических свойств последовательностей, имеющих конечный предел. Сюда входят предел суммы, разности, произведения и частного числовых последовательностей. Свойства пределов последовательностей, связанных неравенствами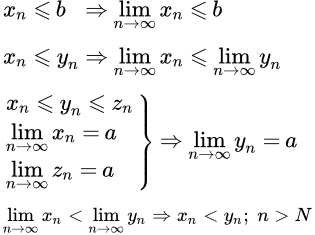 Приводятся формулировки и доказательства теорем и свойств числовых последовательностей, элементы которых связаны неравенствами. Предполагается, что последовательности имеют конечные пределы. Теорема о двух милиционерах
Приводятся формулировки и доказательства теорем и свойств числовых последовательностей, элементы которых связаны неравенствами. Предполагается, что последовательности имеют конечные пределы. Теорема о двух милиционерах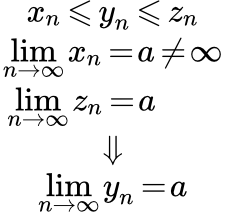 Приводится формулировка и доказательство теоремы о зажатой последовательности, которую в шутку называют «Теоремой о двух милиционерах». Рассмотрены примеры применения этой теоремы. Бесконечно малые последовательности – определение и свойства
Приводится формулировка и доказательство теоремы о зажатой последовательности, которую в шутку называют «Теоремой о двух милиционерах». Рассмотрены примеры применения этой теоремы. Бесконечно малые последовательности – определение и свойства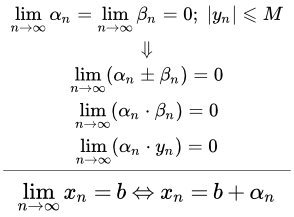 Приводится определение бесконечно малой последовательности. Она обладает свойствами сходящихся последовательностей. Также имеются свойства, характерные только для последовательностей с пределом равным нулю. Приводятся доказательства таких свойств. Рассмотрен пример, в котором нужно доказать, что последовательность бесконечно малая. Определение бесконечно большой последовательности
Приводится определение бесконечно малой последовательности. Она обладает свойствами сходящихся последовательностей. Также имеются свойства, характерные только для последовательностей с пределом равным нулю. Приводятся доказательства таких свойств. Рассмотрен пример, в котором нужно доказать, что последовательность бесконечно малая. Определение бесконечно большой последовательности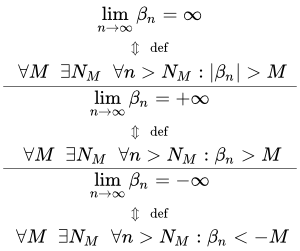 Приводится определение бесконечно большой последовательности. Рассмотрены понятия окрестностей бесконечно удаленных точек. Дано универсальное определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам. Рассмотрены примеры применения определения бесконечно большой последовательности. Свойства бесконечно больших последовательностей
Приводится определение бесконечно большой последовательности. Рассмотрены понятия окрестностей бесконечно удаленных точек. Дано универсальное определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам. Рассмотрены примеры применения определения бесконечно большой последовательности. Свойства бесконечно больших последовательностей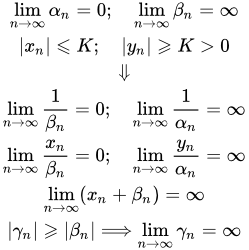 Приводятся формулировки и доказательство свойств бесконечно больших последовательностей. Часть этих свойств связана с бесконечно малыми последовательностями. Бесконечно удаленные точки и их свойства
Приводятся формулировки и доказательство свойств бесконечно больших последовательностей. Часть этих свойств связана с бесконечно малыми последовательностями. Бесконечно удаленные точки и их свойства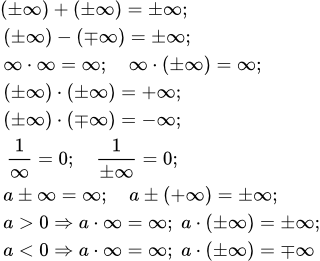 Приводятся определения бесконечно удаленных точек – бесконечности без знака, плюс и минус бесконечности. Дается определение расширенной числовой прямой. Представлены свойства бесконечно удаленных точек и рассмотрен вопрос о доказательстве этих свойств. Приводятся примеры неопределенных операций. Монотонные последовательности
Приводятся определения бесконечно удаленных точек – бесконечности без знака, плюс и минус бесконечности. Дается определение расширенной числовой прямой. Представлены свойства бесконечно удаленных точек и рассмотрен вопрос о доказательстве этих свойств. Приводятся примеры неопределенных операций. Монотонные последовательности Определение и основные свойства монотонной последовательности. Предел ограниченной и неограниченной монотонной последовательности. Теорема Вейерштрасса о пределе монотонной последовательности
Определение и основные свойства монотонной последовательности. Предел ограниченной и неограниченной монотонной последовательности. Теорема Вейерштрасса о пределе монотонной последовательности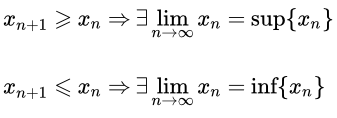 Приводится доказательство теоремы Вейерштрасса о пределе монотонной последовательности. Рассмотрены случаи ограниченной и неограниченной последовательностей. Рассмотрен пример, в котором нужно, применяя теорему Вейерштрасса, доказать сходимость последовательности и найти ее предел. Число e – его смысл и доказательство сходимости последовательности
Приводится доказательство теоремы Вейерштрасса о пределе монотонной последовательности. Рассмотрены случаи ограниченной и неограниченной последовательностей. Рассмотрен пример, в котором нужно, применяя теорему Вейерштрасса, доказать сходимость последовательности и найти ее предел. Число e – его смысл и доказательство сходимости последовательности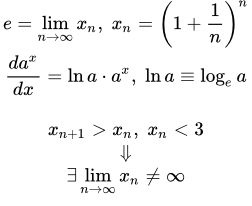 Определение числа e как предела последовательности. Раскрывается смысл и значение числа e в математическом анализе. Приводится доказательство сходимости последовательности к конечному числу тремя способами: разложением в бином Ньютона, используя неравенство Бернулли и применяя вспомогательную последовательность. Лемма о вложенных отрезках (принцип Коши – Кантора)
Определение числа e как предела последовательности. Раскрывается смысл и значение числа e в математическом анализе. Приводится доказательство сходимости последовательности к конечному числу тремя способами: разложением в бином Ньютона, используя неравенство Бернулли и применяя вспомогательную последовательность. Лемма о вложенных отрезках (принцип Коши – Кантора)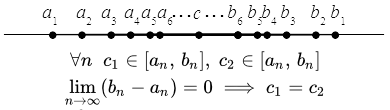 Определение вложенных отрезков. Доказательство леммы Коши – Кантора о вложенных отрезках. Критерий Коши сходимости последовательности
Определение вложенных отрезков. Доказательство леммы Коши – Кантора о вложенных отрезках. Критерий Коши сходимости последовательности Приводятся две формулировки условия Коши для последовательности. Доказательство критерия Коши сходимости последовательности и пример его применения. Подпоследовательности и частичные пределы последовательностей
Приводятся две формулировки условия Коши для последовательности. Доказательство критерия Коши сходимости последовательности и пример его применения. Подпоследовательности и частичные пределы последовательностей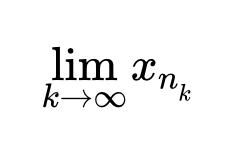 Даны определения подпоследовательности, частичного предела последовательности, верхнего и нижнего частичного предела. Представлены формулировки и доказательства теорем и свойств подпоследовательностей, верхних и нижних частичных пределов последовательностей. Теорема Больцано – Вейерштрасса
Даны определения подпоследовательности, частичного предела последовательности, верхнего и нижнего частичного предела. Представлены формулировки и доказательства теорем и свойств подпоследовательностей, верхних и нижних частичных пределов последовательностей. Теорема Больцано – Вейерштрасса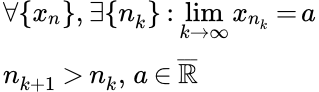 Приводится доказательство теоремы Больцано - Вейерштрасса. Для этого применяется лемма о вложенных отрезках.
Приводится доказательство теоремы Больцано - Вейерштрасса. Для этого применяется лемма о вложенных отрезках.
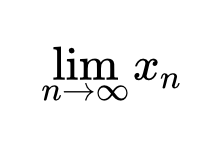 Приводятся формулировки основных теорем и свойств числовых последовательностей, имеющих предел. Содержится определение последовательности и ее предела. Рассмотрены арифметические действия с последовательностями, свойства, связанные с неравенствами, критерии сходимости, свойства бесконечно малых и бесконечно больших последовательностей. Определение числовой последовательности
Приводятся формулировки основных теорем и свойств числовых последовательностей, имеющих предел. Содержится определение последовательности и ее предела. Рассмотрены арифметические действия с последовательностями, свойства, связанные с неравенствами, критерии сходимости, свойства бесконечно малых и бесконечно больших последовательностей. Определение числовой последовательности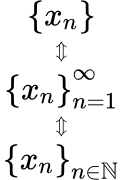 Приводится определение числовой последовательности. Рассмотрены примеры неограниченно возрастающих, сходящихся и расходящихся последовательностей. Рассмотрена последовательность, содержащая все рациональные числа.
Приводится определение числовой последовательности. Рассмотрены примеры неограниченно возрастающих, сходящихся и расходящихся последовательностей. Рассмотрена последовательность, содержащая все рациональные числа.  Способ нумерации рациональных чисел Определение конечного предела последовательности
Способ нумерации рациональных чисел Определение конечного предела последовательности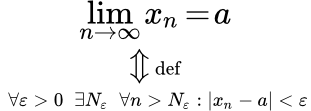 Приводится определение конечного предела последовательности. Рассмотрены связанные с этим свойства и эквивалентное определение. Приводится определение, что точка a не является пределом последовательности. Рассмотрены примеры, в которых доказывается существование предела, используя определение. Основные свойства конечных пределов последовательностей
Приводится определение конечного предела последовательности. Рассмотрены связанные с этим свойства и эквивалентное определение. Приводится определение, что точка a не является пределом последовательности. Рассмотрены примеры, в которых доказывается существование предела, используя определение. Основные свойства конечных пределов последовательностей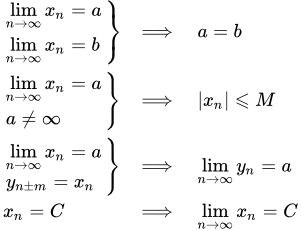 Приводятся формулировки и доказательства основных свойств числовых последовательностей, имеющих конечный предел. Среди них: теорема единственности предела, ограниченность сходящейся последовательности, влияние конечного числа элементов на сходимость. Арифметические свойства конечных пределов последовательностей
Приводятся формулировки и доказательства основных свойств числовых последовательностей, имеющих конечный предел. Среди них: теорема единственности предела, ограниченность сходящейся последовательности, влияние конечного числа элементов на сходимость. Арифметические свойства конечных пределов последовательностей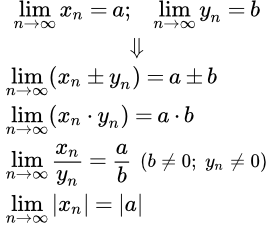 Приводятся формулировки и доказательства арифметических свойств последовательностей, имеющих конечный предел. Сюда входят предел суммы, разности, произведения и частного числовых последовательностей. Свойства пределов последовательностей, связанных неравенствами
Приводятся формулировки и доказательства арифметических свойств последовательностей, имеющих конечный предел. Сюда входят предел суммы, разности, произведения и частного числовых последовательностей. Свойства пределов последовательностей, связанных неравенствами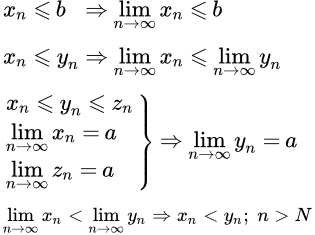 Приводятся формулировки и доказательства теорем и свойств числовых последовательностей, элементы которых связаны неравенствами. Предполагается, что последовательности имеют конечные пределы. Теорема о двух милиционерах
Приводятся формулировки и доказательства теорем и свойств числовых последовательностей, элементы которых связаны неравенствами. Предполагается, что последовательности имеют конечные пределы. Теорема о двух милиционерах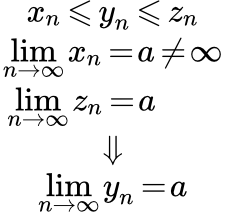 Приводится формулировка и доказательство теоремы о зажатой последовательности, которую в шутку называют «Теоремой о двух милиционерах». Рассмотрены примеры применения этой теоремы. Бесконечно малые последовательности – определение и свойства
Приводится формулировка и доказательство теоремы о зажатой последовательности, которую в шутку называют «Теоремой о двух милиционерах». Рассмотрены примеры применения этой теоремы. Бесконечно малые последовательности – определение и свойства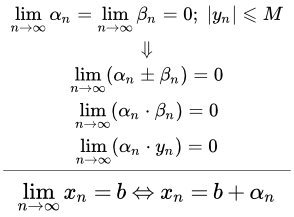 Приводится определение бесконечно малой последовательности. Она обладает свойствами сходящихся последовательностей. Также имеются свойства, характерные только для последовательностей с пределом равным нулю. Приводятся доказательства таких свойств. Рассмотрен пример, в котором нужно доказать, что последовательность бесконечно малая. Определение бесконечно большой последовательности
Приводится определение бесконечно малой последовательности. Она обладает свойствами сходящихся последовательностей. Также имеются свойства, характерные только для последовательностей с пределом равным нулю. Приводятся доказательства таких свойств. Рассмотрен пример, в котором нужно доказать, что последовательность бесконечно малая. Определение бесконечно большой последовательности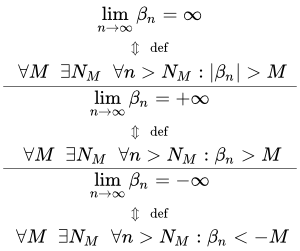 Приводится определение бесконечно большой последовательности. Рассмотрены понятия окрестностей бесконечно удаленных точек. Дано универсальное определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам. Рассмотрены примеры применения определения бесконечно большой последовательности. Свойства бесконечно больших последовательностей
Приводится определение бесконечно большой последовательности. Рассмотрены понятия окрестностей бесконечно удаленных точек. Дано универсальное определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам. Рассмотрены примеры применения определения бесконечно большой последовательности. Свойства бесконечно больших последовательностей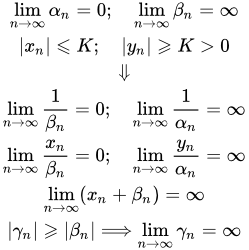 Приводятся формулировки и доказательство свойств бесконечно больших последовательностей. Часть этих свойств связана с бесконечно малыми последовательностями. Бесконечно удаленные точки и их свойства
Приводятся формулировки и доказательство свойств бесконечно больших последовательностей. Часть этих свойств связана с бесконечно малыми последовательностями. Бесконечно удаленные точки и их свойства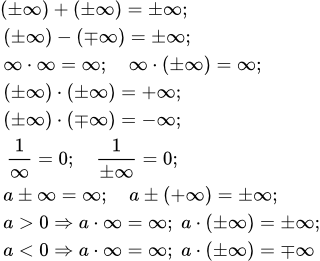 Приводятся определения бесконечно удаленных точек – бесконечности без знака, плюс и минус бесконечности. Дается определение расширенной числовой прямой. Представлены свойства бесконечно удаленных точек и рассмотрен вопрос о доказательстве этих свойств. Приводятся примеры неопределенных операций. Монотонные последовательности
Приводятся определения бесконечно удаленных точек – бесконечности без знака, плюс и минус бесконечности. Дается определение расширенной числовой прямой. Представлены свойства бесконечно удаленных точек и рассмотрен вопрос о доказательстве этих свойств. Приводятся примеры неопределенных операций. Монотонные последовательности Определение и основные свойства монотонной последовательности. Предел ограниченной и неограниченной монотонной последовательности. Теорема Вейерштрасса о пределе монотонной последовательности
Определение и основные свойства монотонной последовательности. Предел ограниченной и неограниченной монотонной последовательности. Теорема Вейерштрасса о пределе монотонной последовательности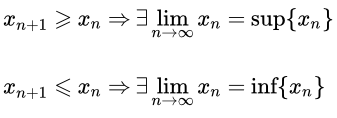 Приводится доказательство теоремы Вейерштрасса о пределе монотонной последовательности. Рассмотрены случаи ограниченной и неограниченной последовательностей. Рассмотрен пример, в котором нужно, применяя теорему Вейерштрасса, доказать сходимость последовательности и найти ее предел. Число e – его смысл и доказательство сходимости последовательности
Приводится доказательство теоремы Вейерштрасса о пределе монотонной последовательности. Рассмотрены случаи ограниченной и неограниченной последовательностей. Рассмотрен пример, в котором нужно, применяя теорему Вейерштрасса, доказать сходимость последовательности и найти ее предел. Число e – его смысл и доказательство сходимости последовательности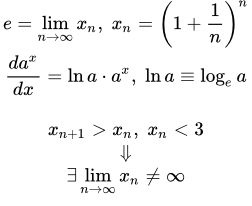 Определение числа e как предела последовательности. Раскрывается смысл и значение числа e в математическом анализе. Приводится доказательство сходимости последовательности к конечному числу тремя способами: разложением в бином Ньютона, используя неравенство Бернулли и применяя вспомогательную последовательность. Лемма о вложенных отрезках (принцип Коши – Кантора)
Определение числа e как предела последовательности. Раскрывается смысл и значение числа e в математическом анализе. Приводится доказательство сходимости последовательности к конечному числу тремя способами: разложением в бином Ньютона, используя неравенство Бернулли и применяя вспомогательную последовательность. Лемма о вложенных отрезках (принцип Коши – Кантора)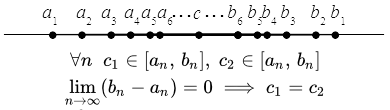 Определение вложенных отрезков. Доказательство леммы Коши – Кантора о вложенных отрезках. Критерий Коши сходимости последовательности
Определение вложенных отрезков. Доказательство леммы Коши – Кантора о вложенных отрезках. Критерий Коши сходимости последовательности Приводятся две формулировки условия Коши для последовательности. Доказательство критерия Коши сходимости последовательности и пример его применения. Подпоследовательности и частичные пределы последовательностей
Приводятся две формулировки условия Коши для последовательности. Доказательство критерия Коши сходимости последовательности и пример его применения. Подпоследовательности и частичные пределы последовательностей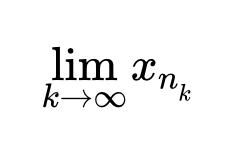 Даны определения подпоследовательности, частичного предела последовательности, верхнего и нижнего частичного предела. Представлены формулировки и доказательства теорем и свойств подпоследовательностей, верхних и нижних частичных пределов последовательностей. Теорема Больцано – Вейерштрасса
Даны определения подпоследовательности, частичного предела последовательности, верхнего и нижнего частичного предела. Представлены формулировки и доказательства теорем и свойств подпоследовательностей, верхних и нижних частичных пределов последовательностей. Теорема Больцано – Вейерштрасса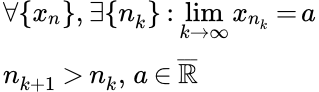 Приводится доказательство теоремы Больцано - Вейерштрасса. Для этого применяется лемма о вложенных отрезках.
Приводится доказательство теоремы Больцано - Вейерштрасса. Для этого применяется лемма о вложенных отрезках. 