y′′+y=x²cos x. Пример решения линейного дифференциального уравнения со специальной неоднородной частью

Пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью y′′+y=x∧2cos x. Приводится подробное решение тремя способами: понижением порядка линейной подстановкой; стандартным способом; стандартным способом, используя комплексные функции.

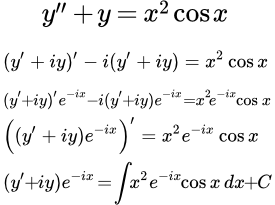
Условие примера

Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами и специальной неоднородной частью в виде произведения многочлена второй степени и косинуса:
(1)   y^′′ + y = x² cos x . 

1. Самое простое решение примера

Применим метод понижения порядка линейной заменой переменных.

Делаем подстановку
(1.1)   u = y^′ + iy , 
где i – комплексная единица, i²  = – 1 .  тогда уравнение (1) примет вид:
(1.2)   u^′ – iu = x² cos x . 
Действительно, u^′ – iu = y^′′ + iy^′ – i (y^′ + iy )  =  y^′′ – i² y = y^′′ + y .  Все правильно.

Решаем линейное неоднородное уравнение первого порядка (1.2) с помощью интегрирующего множителя. Умножим на e^– ix  и выделим полный дифференциал:
u^′e^– ix  – iue^– ix  = x² e^– ix cos x ; 
u^′e^– ix  + u (e^– ix ) ^′ = x² e^– ix cos x ; 
(ue^– ix ) ^′ = x² e^– ix cos x . 
Интегрируем:
(1.3)   ue^– ix  = ∫ x² e^– ix cos x dx + C . 

Вычисляем интеграл. Для этого, с помощью формулы Эйлера, выразим косинус через экспоненту:
e^– ix cos x = e^– ix e^ix  + e^– ix 2 =  1 + e^– 2ix 2  . 
Тогда интеграл примет вид:
(1.4)   I = ∫ x² e^– ix cos x dx =  ∫ x² 1 + e^– 2ix 2  dx = 
 12 ∫ x² dx + 12 ∫ x² e^– 2ix dx =  12 I₁  + 12 I₂  . 

Первый интеграл табличный:
(1.5)   I₁  = ∫ x² dx = 12 + 1 x^2 + 1  = x³ 3  . 

Второй интеграл интегрируем по частям:
e^– 2ix dx = 1– 2i e^– 2ix d (– 2ix )  =  i– 2i²  d (e^– 2ix )  = i2 d (e^– 2ix )  ; 
∫ e^– 2ix dx = i2 ∫ d (e^– 2ix )  = i2 e^– 2ix  ; 
∫ xe^– 2ix dx = i2 ∫ x d (e^– 2ix )  =  i2 ( xe^– 2ix  – ∫ e^– 2ix dx  )  = 
 i2 ( xe^– 2ix  – i2 e^– 2ix  )  =  ( ix2 + 14  ) e^– 2ix  ; 
I₂  = ∫ x² e^– 2ix dx =  i2 ∫ x² d (e^– 2ix )  =  i2 ( x² e^– 2ix  – ∫ (x² ) ^′e^– 2ix dx  )  = 
 i2 x² e^– 2ix  – i2 ∫ 2xe^– 2ix dx =  i2 x² e^– 2ix  – i ∫ xe^– 2ix dx = 
 i2 x² e^– 2ix  – i ( ix2 + 14  ) e^– 2ix  =  ( ix² 2 + x2 – i4  ) e^– 2ix  ; 
(1.6)   I₂  = ( ix² 2 + x2 – i4  ) e^– 2ix  . 

Подставляем (1.5)  и (1.6)  в (1.4), а затем в (1.3):
ue^– ix  = I + C = 12 I₁  + 12 I₂  + C =  12 ⋅ x³ 3 +  12 ( ix² 2 + x2 – i4  ) e^– 2ix  + C ; 
(1.7)   ue^– ix  =  x³ 6 + ( ix² 4 + x4 – i8  ) e^– 2ix  + C . 
Теперь учтем, что постоянная интегрирования C является комплексным числом. Поэтому запишем ее в виде C = C₁  + iC₂  ,  где C₁ ,  C₂  – действительные числа. Умножим (1.7) на e^ix  .  Также учтем, что согласно (1.1), u = y^′ + iy  : 
(1.8)   u = y^′ + iy = x³ 6 e^ix  +  ( ix² 4 + x4 – i8  ) e^– ix  +  (C₁  + iC₂ ) e^ix  . 

Учтем тот факт, что исходное уравнение (1) имеет действительное решение. Поэтому функции y и y^′ действительные. Тогда, чтобы найти y ,  нам нужно найти мнимую часть от выражения (1.8) справа. Выделяем действительную и мнимую части:
y^′ + iy = x³ 6 (cos x + i sin x )  +  ( ix² 4 + x4 – i8  ) (cos x – i sin x )  + 
 (C₁  + iC₂ ) (cos x + i sin x )  =  x³ 6 cos x + x4 cos x +  ( x² 4 – 18  ) sin x + 
 C₁ cos x – C₂ sin x +  i [x³ 6 sin x + ( x² 4 – 18  ) cos x –  x4 sin x + C₂ cos x + C₁ sin x  ]  . 
Отсюда получаем решение уравнения:
y = Im (y^′ + iy )  = x³ 6 sin x +  ( x² 4 – 18  ) cos x – x4 sin x +  C₂ cos x + C₁ sin x = 
 x² 4 cos x + ( x³ 6 – x4  ) sin x +  ( C₂  – 18  ) cos x + C₁ sin x . 

Преобразуем постоянные интегрирования: C₂  – 18 → C₁ ;  C₁  → C₂  . 

Ответ

y = x² 4 cos x + ( x³ 6 – x4  ) sin x +  C₁ cos x + C₂ sin x . 

2. Стандартное решение

Теперь решим наше уравнение (1)   стандартным методом. Этот метод применим для решения линейных дифференциальных уравнений n-го порядка с постоянными коэффициентами со специальной неоднородностью, которые имеют следующий вид:
a_n y^(n )  + ⋅ ⋅ ⋅ + a₂ y^′′ + a₁ y^′ + a₀ y = e^αx  ⋅ (P_s1 (x ) cos (βx )  + Q_s2 (x ) sin (βx ) )  , 
где P_s1 (x ) ,  Q_s2  – многочлены степеней s₁  и s₂  ,  соответственно:
P_s1 (x )  = p₀  + p₁ x + ⋅ ⋅ ⋅ + p_{s1  – 1} x^{s₁  – 1}  + p_s1 x^s₁  ; 
Q_s2 (x )  = q₀  + q₁ x + ⋅ ⋅ ⋅ + q_{s2  – 1} x^{s₂  – 1}  + q_s2 x^s₂  ; 
p₀ ,  p₁ , ... ,  p_s1 ,  q₀ ,  q₁ , ... ,  q_s2  – известные коэффициенты.

В нашем случае, уравнение (1) второго порядка, a₂  = 1,  a₁  = 0,  a₀  = 1 ,  α = 0,  β = 1,  s₁  = 2,   p₀  = p₁  = 0,  p₂  = 1,  Q_s2 (x )  = 0 . 

2.1 Общее решение однородного уравнения

Вначале находим общее решение однородного уравнения. Для этого отбрасываем в (1) правую неоднородную часть. Получаем однородное уравнение, в котором, чтобы не было путаницы, заменим y на y₀   : 
(2.1)   y^′′₀  + y₀  = 0 . 

Ищем решение в виде y₀  = e^kx  .  Составляем характеристическое уравнение:
k²  + 1 = 0 . 
Оно имеет комплексные корни:
k₁  = – i;  k₂  = i . 
Им соответствует фундаментальная система решений:
y₁ (x )  = cos x,  y₂ (x )  = sin x . 
Общее решение однородного уравнения (2.1):
y₀  = C₁  y₁  + C₂  y₂  =  C₁ cos x + C₂ sin x . 

2.2 Частное решение неоднородного уравнения

Поскольку характеристическое уравнение имеет корень k = i кратности p = 1 ,  и неоднородная часть имеет множитель cos x ,  то частное решение Y ищем в виде
Y (x )  = x^p  ((Ax²  + Bx + D ) cos x +  (Ex²  + Fx + G ) sin x  )  ; 
(2.2)   Y (x )  = (Ax³  + Bx²  + Dx ) cos x +  (Ex³  + Fx²  + Gx ) sin x . 
Здесь A,  B,  D,  E,  F,  G – действительные коэффициенты, которые нужно определить.

Для определения коэффициентов A,  B,  D,  E,  F,  G ,  подставим частное решение (2.2) в исходное уравнение, и приравняем левую и правую части.

Найдем производные от Y . Поскольку нам нужна только производная второго порядка, то применим формулу Лейбница:
(uv ) ^′′ = u^′′ + 2u^′v^′ + v^′′ . 

Дифференцируем. Для удобства введем обозначения:
P = Ax³  + Bx²  + Dx;   Q = Ex³  + Fx²  + Gx . 
Тогда Y = P cos x + Q sin x ; 
P^′ = 3Ax²  + 2Bx + D;   P^′′ = 6Ax + 2B ; 
Q^′ = 3Ex²  + 2Fx + G;   Q^′′ = 6Ex + 2F ; 
(cos x ) ^′ = – sin x;   (cos x ) ^′′ = – cos x ; 
(sin x ) ^′ = cos x;   (sin x ) ^′′ = – sin x ; 
Y^′′ = P^′′ cos x + 2P^′(cos x ) ^′ +  P (cos x ) ^′′ + Q^′′ sin x +  2Q^′(sin x ) ^′ + Q (sin x ) ^′′ = 
 (6Ax + 2B ) cos x –  2(3Ax²  + 2Bx + D ) sin x –  (Ax³  + Bx²  + Dx ) cos x + 
 (6Ex + 2F ) sin x +  2(3Ex²  + 2Fx + G ) cos x –  (Ex³  + Fx²  + Gx ) sin x ; 
Y^′′ = (– Ax³  + (– B + 6E ) x²  +  (6A – D + 4F ) x + 2B + 2G  ) cos x + 
 (– Ex³  + (– 6A – F ) x²  +  (– 4B + 6E – G ) x – 2D + 2F  ) sin x . 

Подставляем в (1) и выполняем преобразования:
Y^′′ + Y = x² cos x ; 
(– Ax³  + (– B + 6E ) x²  +  (6A – D + 4F ) x +  2B + 2G  ) cos x + 
 (– Ex³  + (– 6A – F ) x²  +  (– 4B + 6E – G ) x –  2D + 2F  ) sin x + 
 (Ax³  + Bx²  + Dx ) cos x +  (Ex³  + Fx²  + Gx ) sin x = x² cos x ; 
(6Ex²  + (6A + 4F ) x +  2B + 2G  ) cos x + 
 (– 6Ax²  + (– 4B + 6E ) x –  2D + 2F  ) sin x = x² cos x . 

Сравнивая левую и правую части, получаем систему уравнений:
6E = 1;  6A + 4F = 0;   2B + 2G = 0 ; 
– 6A = 0;   – 4B + 6E = 0;   – 2D + 2F = 0 . 
Решаем ее.
A = 0;  E = 1 / 6;   F = – 64 A = 0;  
 B = 64 E = 14 ;   G = – B = – 14 ;  D = F = 0 . 

Отсюда получаем частное решение исходного уравнения:
Y = (Ax³  + Bx²  + Dx ) cos x +  (Ex³  + Fx²  + Gx ) sin x = 
 14 x² cos x + ( 16 x³  – 14 x  ) sin x . 
Общее решение исходного уравнения:
y = y₀  + Y . 

Ответ

y = C₁ cos x + C₂ sin x +  x² 4 cos x + ( x³ 6 – x4  ) sin x . 

3. Стандартное решение с использованием комплексных функций

3.1. Описание метода

Суть этого метода заключается в том, чтобы выполнять вычисления, используя экспоненту вместо синусов и косинусов. При таком подходе, в ряде случаев получаются более простые преобразования. При этом нам нужно использовать комплексные числа и элементарные сведения из области функций комплексного переменного.

Рассмотрим комплексную функцию w = w (z )  ,  зависящую от комплексной переменной
z = x + iy , 
где x,  y – действительные числа. Ее можно записать в виде суммы действительной и мномой частей:
w = u + iv , 
где u,  v – действительные функции от комплексной переменной z .  Например:
e^iz  = e^{i (x + iy )}  = e^ix – y  = e^ix e^– y  =  e^– y (cos x + i sin x )  =  e^– y cos x + ie^– y sin x = u + iv . 
Отсюда u = e^– y cos x;  v = e^– y sin x . 

Далее мы будем считать, что множеством определения всех функций является множество действительных чисел. То есть будем считать, что комплексная переменная z принимает только действительные значения: z = x;  y = 0 . 

Пусть функция w является решением линейного неоднородного уравнения:
(3.1)   a_n w^(n )  + a_n – 1 w^{(n – 1 )}  + ⋅ ⋅ ⋅ + a₁ w^′ + a₀  = F (x )  , 
где a_i  – действительные коэффициенты (или действительные функции от действительной переменной x); F (x )  =  f (x )  + ig (x )  – комплексная функция;  f (x )  и g (x )  – действительные функции. Тогда действительная u и мнимая v части функции w удовлетворяют дифференциальным уравнениям:
(3.2)   a_n u^(n )  + a_n – 1 u^{(n – 1 )}  + ⋅ ⋅ ⋅ + a₁ u^′ + a₀  =  f (x )  = Re F (x )  ; 
(3.3)   a_n v^(n )  + a_n – 1 v^{(n – 1 )}  + ⋅ ⋅ ⋅ + a₁ v^′ + a₀  = g (x )  = Im F (x )  . 

Для доказательства подставим w = u + iv в (3.1):
a_n (u^(n )  + iv^(n ) )  +  a_n – 1 (u^{(n – 1 )}  + iv^{(n – 1 )} )  + ⋅ ⋅ ⋅ + a₁ (u^′ + iv^′ )  + a₀  =  f (x )  + ig (x )  . 
Поскольку коэффициенты a_i  действительные, то, отделяя действительную и мнимую части, получаем, что функции u и v удовлетворяют дифференциальным уравнениям (3.2)  и  (3.3).

3.2. Применение метода

Применим этот прием к нашему уравнению (1). Возьмем комплексную функцию F (x )  = x² e^ix  = x² cos x + ix² sin x ,  и рассмотрим уравнение:
(3.4)   w^′′ + w = x² e^ix  . 
Тогда действительная часть u комплексного решения w = u + iv этого уравнения будет удовлетворять исходному уравнению (1):
u^′′ + u = x² cos x . 

Для решения (3.4) мы используем стандартный метод ⇑.

3.2.1. Общее решение однородного уравнения

Находим общее решение однородного уравнения. Отбрасываем в (3.4) правую неоднородную часть. Получаем однородное уравнение:
w^′′₀  + w₀  = 0 . 

Ищем решение в виде w₀  = e^kx  .  Получаем характеристическое уравнение:
(3.5)   k²  + 1 = 0 . 
Оно имеет комплексные корни
k₁  = – i;  k₂  = i . 
Им соответствует фундаментальная система решений
w₁ (x )  = e^k₁ x  = e^– ix ,   w₂ (x )  = e^k₂ x  = e^ix  . 
Общее решение однородного уравнения:
(3.6)   w₀  = ^~C₁  w₁  + ^~C₂  w₂  =  ^~C₁ e^– ix  + ^~C₂ e^ix  , 
где ^~C₁  и ^~C₂  – комплексные постоянные.

Выделим в общем решении действительную и мнимую части. Для этого выразим комплексные постоянные ^~C₁ ,  ^~C₂  через действительные C_1r ,  C_1i ,  C_2r ,  C_2i   : 
^~C₁  = C_1r  + iC_1i ;  ^~C₂  = C_2r  + iC_2i  . 
Подставим в (3.6) и применим формулу Эйлера:
w₀  = (C_1r  + iC_1i ) (cos x – i sin x )  +  (C_2r  + iC_2i ) (cos x + i sin x )  ; 
w₀  = (C_1r  + C_2r ) cos x +  (C_1i  – C_2i ) sin x +  i [(C_1i  + C_2i ) cos x +  (C_2r  – C_1r ) sin x ]  . 
Заменим постоянные C_1r  + C_2r  → C₁ ,  C_1i  – C_2i  → C₂ ,   C_1i  + C_2i  → C₃ ,  C_2r  – C_1r  → C₄   : 
(3.7)   w₀  = C₁ cos x + C₂ sin x +  i (C₃ cos x + C₄ sin x )  . 

3.2.2. Частное решение неоднородного уравнения

Находим частное решение уравнения (3.4). Неоднородная часть является экспонентой, умноженной на многочлен второй степени. Поскольку k = i является корнем характеристического уравнения (3.5) кратности p = 1 ,  то частное решение ищем в виде:
W = x^p (Ax²  + Bx + D ) e^ix  =  x (Ax²  + Bx + D ) e^ix  ; 
W = (Ax³  + Bx²  + Dx ) e^ix  . 

Находим производную второго порядка от W , применяя формулу Лейбница:
(uv ) ^′′ = u^′′ + 2u^′v^′ + v^′′ . 

Дифференцируем. При этом используем обозначение:
P = Ax³  + Bx²  + Dx . 
Тогда W = Pe^ix  ; 
P^′ = 3Ax²  + 2Bx + D;   P^′′ = 6Ax + 2B ; 
(e^ix ) ^′ = ie^ix ;   (e^ix ) ^′′ = i (e^ix ) ^′ = i ⋅ ie^ix  = – e^ix  ; 
W^′′ =  P^′′e^ix  + 2P^′(e^ix ) ^′ + P (e^ix ) ^′′ = 
 (6Ax + 2B ) e^ix  +  2(3Ax²  + 2Bx + D ) ie^ix  –  (Ax³  + Bx²  + Dx ) e^ix  ; 
W^′′ = (– Ax³  + (6iA – B ) x²  +  (6A + 4iB – D ) x + 2B + 2iD  ) e^ix  . 

Подставляем в (3.4):
W^′′ + W = x² e^ix  ; 
(– Ax³  + (6iA – B ) x²  +  (6A + 4iB – D ) x + 2B + 2iD  ) e^ix  + 
 (Ax³  + Bx²  + Dx ) e^ix  = x² e^ix  ; 
6iAx²  + (6A + 4iB ) x +  2B + 2iD = x²  . 

Сравнивая левую и правую части, получаем систему уравнений:
6iA = 1;  6A + 4iB = 0;   2B + 2iD = 0 . 
Отсюда
A = 16i = i6i²  = – i6 ;   B = – 64i A = 64i i6 = 14 ;  
 D = – Bi = – 14i = – i4i²  = i4  . 

Частное решение:
W = (Ax³  + Bx²  + Dx ) e^ix  =  ( – ix³ 6 + x² 4 + ix4  ) e^ix  . 
Разделяем действительную и мнимую части:
W =  ( – ix³ 6 + x² 4 + ix4  )  ⋅  (cos x + i sin x )  =  x² 4 cos x + ( x³ 6 – x4  ) sin x + 
 i [( – x³ 6 + x4  ) cos x + x² 4 sin x  ]  . 
Прибавляя общее решение (3.7) однородного уравнения, получаем общее решение комплексного неоднородного уравнения (3.4):
w = w₀  + W =  C₁ cos x + C₂ sin x +  i (C₃ cos x + C₄ sin x )  + 
 x² 4 cos x + ( x³ 6 – x4  ) sin x +  i [( – x³ 6 + x4  ) cos x + x² 4 sin x  ]  . 
Отделяя действительную часть, получаем общее решение исходного уравнения (1):
y = Re w = C₁ cos x + C₂ sin x +  x² 4 cos x + ( x³ 6 – x4  ) sin x . 

Ответ

y = C₁ cos x + C₂ sin x +  x² 4 cos x + ( x³ 6 – x4  ) sin x . 

Автор: Олег Одинцов.     Опубликовано: 12-03-2021