Дифференциальные уравнения первого порядка, не разрешенные относительно производной

Приводятся основные виды обыкновенных дифференциальных уравнений первого порядка, не разрешенные относительно производной. Разобраны самые простые из них и даны ссылки на страницы, содержащие методы их решения с примерами.

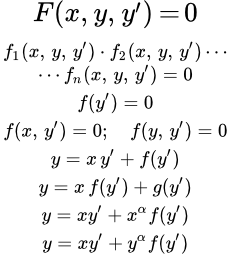
Дифференциальные уравнения, которые удается разрешить относительно производной

Сначала нужно проверить, не удастся ли уравнение решить относительно производной. Если уравнение удается разрешить относительно производной, то оно сводится к одному из ранее рассмотренных типов.

Пример

Решить уравнение:
(1)  

Решение

Решим это уравнение относительно производной. Возводим уравнение (1) в квадрат:
.
Или:
;
.
Поскольку , то .
Извлекаем квадратный корень. Получаем два значения:
(2)   .
Из уравнения (1) следует, что .
Поэтому при , . В уравнении (2) выбираем верхний знак “+”.
При , . В уравнении (2) выбираем нижний знак “–”.

Интегрируем, применяя таблицу интегралов:
(3)   .
Поскольку верхний знак “+” относится к , а нижний знак “–” относится к , то
.
Тогда
.

Теперь объясним, как мы вынесли за знак логарифма в (3).
Применим формулу:
.
Приравняем модули левой и правой частей:
.
Подставим ; :
;
;
;
.
Логарифмируем, применяя свойства логарифмов:
.
Отсюда
.

Ответ

.

Дифференциальные уравнения, допускающие разложение на множители

Также нужно проверить, не удастся ли представить уравнение в виде произведения множителей:
.
Если такое разложение возможно, то последовательно решают уравнения, составленные из сомножителей:
;
;
;
....................
.

Виды не разрешенных уравнений, допускающих решение

Далее приведены виды не разрешенных относительно производной дифференциальных уравнений первого порядка, допускающих решение.

Уравнения, не содержащие x и y

Это уравнения, которые не содержат в явном виде независимую и зависимую переменные:
.
См. Уравнения, содержащие только производную.

Уравнения, не содержащие x или y

Это уравнения, которые не содержат в явном виде либо независимую переменную , либо зависимую переменную :
;   или   .
См. Уравнения, не содержащие одну из переменных в явном виде.

Уравнения, разрешенные относительно y

Уравнения Клеро

См. Дифференциальное уравнение Клеро.

Уравнения Лагранжа

См. Дифференциальное уравнение Лагранжа.

Уравнения, приводящиеся к уравнению Бернулли

;
.
См. Дифференциальное уравнение, не разрешенное относительно производной, приводящееся к уравнению Бернулли.

Автор: Олег Одинцов.     Опубликовано: 18-08-2012   Изменено: 06-03-2016