Арифметические свойства предела функции
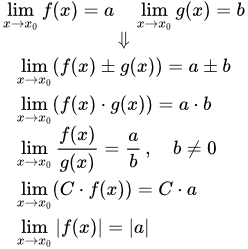
Формулировки арифметических свойств конечных пределов
Пусть функции и определены на некоторой проколотой окрестности конечной или бесконечно удаленной точки . И пусть существуют конечные пределы:
и .
Тогда существует предел суммы (или разности) двух функций, и он равен сумме (или разности) их пределов:
; доказательство ⇓
существует предел произведения функций и он равен произведению их пределов:
; доказательство ⇓
если b ≠ 0, то существует предел частного функций и он равен частному их пределов:
. доказательство ⇓
В частности, если C – постоянная, то есть заданное число, то постоянную можно выносить за знак предела:
; доказательство ⇓
Предел абсолютного значения функции равен абсолютному значению ее предела:
если , то . Доказательство ⇓
Мы привели арифметические свойства пределов для двух функций. Методом математической индукции легко показать, что они выполняются и для конечного числа функций.
Так, если n функций имеют конечные пределы в точке , то предел их суммы или разности равен сумме или разности их пределов; предел произведения равен произведению пределов.
В частности, если существует конечный предел , то предел от функции , возведенной в натуральную степень n, равен пределу этой функции в степени n:
.
Такое равенство справедливо не только для натуральных показателей степени n, но здесь мы рассматриваем только следствия арифметических свойств.
Арифметических свойства бесконечно больших и бесконечно малых функций
Подобные свойства имеются и когда предел одной из функций равен бесконечности или нулю. Ниже мы приводим эти свойства.
Пусть существуют пределы функций
и .
И пусть, при , функция является бесконечно малой:
, а функция – бесконечно большой:
.
Тогда существует пределы суммы и разности:
;
существуют пределы произведений:
;
существуют пределы частного:
.
Доказательство
Символически эти свойства можно записать так:
;
;
,
где .
Эти свойства выполняются и в случае, если функции и не имеют пределов при . При этом должна существовать проколотая окрестность точки , на которой функция ограничена: , а функция ограничена снизу по абсолютной величине положительным числом: .
Доказательство арифметических свойств
Теорема о пределе суммы (или разности) двух функций
Все формулировки ⇑ Пусть существуют конечные пределы функций:
и .
Тогда существует предел суммы (или разности) двух функций, и он равен сумме (или разности) их пределов:
.
Доказательство
Поскольку существуют пределы и , то существует такая проколотая окрестность точки , на которой функции и определены. Используем определение предела функции по Гейне. Пусть есть произвольная последовательность, сходящаяся к точке , элементы которой принадлежат проколотой окрестности . Тогда определены последовательности и . Поскольку и , то эти последовательности имеют пределы и .
Рассмотрим функцию , которая является суммой (или разностью) функций и . Используя свойство предела суммы и разности числовых последовательностей, имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к и элементы которой принадлежат проколотой окрестности , то, согласно определению предела функции по Гейне,
, или
.
Теорема о пределе произведения двух функций
Все формулировки ⇑ Пусть существуют конечные пределы функций:
и .
Тогда существует предел произведения функций и он равен произведению их пределов:
.
Доказательство
Поскольку существуют пределы и , то существует такая проколотая окрестность точки , на которой функции и определены. Используем определение предела функции по Гейне. Пусть есть произвольная последовательность, сходящаяся к точке , элементы которой принадлежат проколотой окрестности . Тогда определены последовательности и . Поскольку и , то эти последовательности имеют пределы и .
Рассмотрим функцию . Используя свойство предела произведения числовых последовательностей, имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , элементы которой принадлежат проколотой окрестности , то, согласно определению предела функции по Гейне,
, или
.
Теорема о пределе частного двух функций
Все формулировки ⇑ Пусть существуют конечные пределы функций:
и .
Тогда, если b ≠ 0, то существует предел частного функций и он равен частному их пределов:
.
Доказательство
Поскольку существуют пределы и , то существует такая проколотая окрестность точки , на которой функции и определены. Используем определение предела функции по Гейне. Пусть есть произвольная последовательность, сходящаяся к точке , элементы которой принадлежат проколотой окрестности, на которой определены функции и . Тогда определены последовательности и . Поскольку и , то эти последовательности имеют пределы и .
Рассмотрим функцию . По условию, . Воспользуемся теоремой об ограниченности снизу функции, имеющей конечный ненулевой предел. Согласно этой теореме, существует такая проколотая окрестность точки , на которой . Отсюда следует, что существует такая проколотая окрестность этой точки, на которой .
Пусть есть проколотая окрестность точки , на которой определены функции и , и на которой . Используя свойство предела частного числовых последовательностей, имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , элементы которой принадлежат проколотой окрестности , то, согласно определению предела функции по Гейне,
, или
.
Теорема о вынесении постоянной за знак предела
Все формулировки ⇑ Пусть существует конечный предел функции:
.
И пусть C – постоянная, то есть заданное число. Тогда постоянную можно выносить за знак предела:
.
Доказательство
Введем постоянную функцию , значения которой для всех x равны некоторому числу C. Согласно теореме о пределе постоянной функции,
.
Используя доказанное только что свойство предела произведения двух функций, имеем:
.
Теорема о пределе абсолютного значения функции
Все формулировки ⇑ Пусть существует конечный предел функции:
.
Тогда существует предел абсолютного значения функции, равный абсолютному значению ее предела:
.
Доказательство
Поскольку существует предел , то существует такая проколотая окрестность точки , на которой функция определена. Используем определение предела функции по Гейне. Пусть есть произвольная последовательность, сходящаяся к точке , элементы которой принадлежат проколотой окрестности . Тогда определена последовательность . Поскольку , то эта последовательность имеет предел .
Используя свойство предела последовательности, состоящей из элементов, взятых по модулю, имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , элементы которой принадлежат проколотой окрестности , то, согласно определению предела функции по Гейне,
.
Пример
Все примеры Найти предел функции
.
Решение
Воспользуемся тем, что .
Последовательно применяем арифметические свойства пределов функции.
;
;
;
;
.
Ответ
.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
