Теорема о пределе промежуточной функции
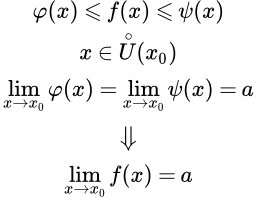
Формулировка
Эту теорему также называют теоремой о пределе зажатой функции, или теоремой о двух милиционерах для функции.
Пусть на некоторой проколотой окрестности конечной, или бесконечно удаленной точки x0 выполняются неравенства:
.
И пусть существуют конечные (или бесконечные определенного знака) равные пределы:
. Тогда существует предел функции :
.
Доказательство
Пусть есть произвольная последовательность, сходящаяся к : . И пусть ее элементы принадлежат проколотой окрестности точки , на которой выполняются неравенства
(1) .
Рассмотрим последовательности , и . По условию теоремы,
.
Тогда, согласно определению предела функции по Гейне, последовательности и имеют пределы:
, .
В силу (1), элементы последовательностей связаны неравенствами:
.
Тогда, согласно теореме о промежуточных последовательностях, существует предел последовательности :
.
Поскольку есть произвольная последовательность, сходящаяся к , то, согласно определению предела функции по Гейне,
.
Теорема доказана.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
