Предел последовательности – основные теоремы и свойства
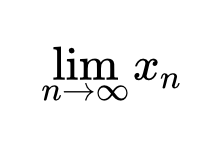
Определение последовательности
- Числовая последовательность
- – это закон (правило), согласно которому, каждому натуральному числу ставится в соответствие число .
Число называют n-м членом или элементом последовательности.
Обозначают последовательность так: .
Далее мы будем считать, что элементами последовательности являются действительные числа.
- Ограниченная последовательность
- Последовательность называется ограниченной, если существует такое число M, что для всех действительных n.
- Верхняя грань последовательности
- Верхней гранью последовательности называют наименьшее из чисел, ограничивающее последовательность сверху. То есть это такое число s, для которого для всех n и для любого , найдется такой элемент последовательности , превосходящий s′: .
- Нижняя грань последовательности
- Нижней гранью последовательности называют наибольшее из чисел, ограничивающее последовательность снизу. То есть это такое число i, для которого для всех n и для любого , найдется такой элемент последовательности , меньший i′: .
Верхнюю грань также называют точной верхней границей, а нижнюю грань – точной нижней границей. Понятия верхней и нижней граней справедливы не только к последовательностям, но и к любым множествам действительных чисел.
Определение предела последовательности
- Предел последовательности
- Число a называется пределом последовательности , если для любого положительного числа существует такое натуральное число N, зависящее от , что для всех натуральных выполняется неравенство
.
Предел последовательности обозначается так:
.
Или при .
С помощью логических символов существования и всеобщности определение предела можно записать следующим образом:
.
- Эпсилон окрестность точки
- ε - окрестностью точки a называется открытый интервал (a – ε, a + ε).
Таким же образим можно ввести понятия дельта, сигма, и т.д. окрестностей.
- Сходящаяся последовательность
- – это последовательность, у которой существует предел .
Также говорят, что последовательность сходится к a.
- Расходящаяся последовательность
- – это последовательность, не имеющая предела.
Точка a не является пределом последовательности , если существует такое , что для любого натурального n существует такое натуральное m > n, что
.
.
Это означает, что можно выбрать такую ε - окрестностью точки a, за пределами которой будет находиться бесконечное число элементов последовательности.
Свойства конечных пределов последовательностей
Основные свойства
Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.
Если число a не является пределом последовательности , то существует такая окрестность точки a, за пределами которой находится бесконечное число элементов последовательности.
Теорема единственности предела числовой последовательности. Если последовательность имеет предел, то он единственный.
Если последовательность имеет конечный предел, то она ограничена.
Если каждый элемент последовательности равен одному и тому же числу C: , то эта последовательность имеет предел, равный числу C.
Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.
Арифметические действия с пределами
Пусть существуют конечные пределы и последовательностей и . И пусть C – постоянная, то есть заданное число. Тогда
;
;
;
, если .
В случае частного предполагается, что для всех n.
Если , то .
Свойства, связанные с неравенствами
Если и элементы последовательности, начиная с некоторого номера, удовлетворяют неравенству , то и предел a этой последовательности удовлетворяет неравенству .
Если и элементы последовательности, начиная с некоторого номера, принадлежат замкнутому интервалу (сегменту) , то и предел a также принадлежит этому интервалу: .
Если и и элементы последовательностей, начиная с некоторого номера, удовлетворяют неравенству , то .
Если и, начиная с некоторого номера, , то .
В частности, если, начиная с некоторого номера, , то
если , то ;
если , то .
Если и , то .
Пусть и . Если a < b, то найдется такое натуральное число N, что для всех n > N выполняется неравенство .
Бесконечно большая и бесконечно малая последовательности
Бесконечно малая последовательность
- Бесконечно малая последовательность
- – это последовательность, предел которой равен нулю:
.
Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.
Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Для того, чтобы последовательность имела предел a, необходимо и достаточно, чтобы , где – бесконечно малая последовательность.
Бесконечно большая последовательность
Определение
- Бесконечно большая последовательность
- – это последовательность, имеющая бесконечно большой предел. То есть если для любого положительного числа существует такое натуральное число N, зависящее от , что для всех натуральных выполняется неравенство
.
В этом случае пишут
.
Или при .
Говорят, что стремится к бесконечности.
Если , начиная с некоторого номера N, то
.
Если же , то
.
Свойства
Если последовательность являются бесконечно большой, то, начиная с некоторого номера N, определена последовательность , которая является бесконечно малой. Если являются бесконечно малой последовательностью с отличными от нуля элементами, то последовательность является бесконечно большой.
Если последовательность бесконечно большая, а последовательность ограничена, то
.
Если абсолютные значения элементов последовательности ограничены снизу положительным числом ( ), а – бесконечно малая с неравными нулю элементами, то
.
См. также Бесконечно удаленные точки и их свойства
Критерии сходимости последовательностей
Монотонные последовательности
Определение
- Строго возрастающая последовательность
- – это последовательность, для всех элементов которой выполняются неравенства:
.
Аналогичными неравенствами определяются другие монотонные последовательности.
- Строго убывающая последовательность:
- .
- Неубывающая последовательность:
- .
- Невозрастающая последовательность:
- .
Отсюда следует, что строго возрастающая последовательность также является неубывающей. Строго убывающая последовательность также является невозрастающей.
- Монотонная последовательность
- – это неубывающая или невозрастающая последовательность.
Свойства
Монотонная последовательность ограничена, по крайней мере, с одной стороны значением . Неубывающая последовательность ограничена снизу: . Невозрастающая последовательность ограничена сверху: .
Теорема Вейерштрасса. Для того чтобы неубывающая (невозрастающая) последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной сверху (снизу ). Здесь M – некоторое число.
Доказательство
Поскольку любая неубывающая (невозрастающая) последовательность ограничена снизу (сверху), то теорему Вейерштрасса можно перефразировать следующим образом:
Для того чтобы монотонная последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной: .
Монотонная неограниченная последовательность имеет бесконечный предел, равный для неубывающей и для невозрастающей последовательности.
Критерий Коши сходимости последовательности
- Условие Коши
- Последовательность удовлетворяет условию Коши, если для любого существует такое натуральное число , что для всех натуральных чисел n и m, удовлетворяющих условию , выполняется неравенство
.
- Фундаментальная последовательность
- – это последовательность, удовлетворяющая условию Коши.
Критерий Коши сходимости последовательности. Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
Доказательство
Подпоследовательности
Теорема Больцано – Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность. А из любой неограниченной последовательности – бесконечно большую подпоследовательность, сходящуюся к или к .
Доказательство
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
В.А. Зорич. Математический анализ. Часть 1. Москва, 1997.
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Москва, 2005.
Автор: Олег Одинцов. Опубликовано: Изменено:
