Методы решения физико-математических задач

Бесконечно малые последовательности – определение и свойства

Свойства бесконечно малых последовательностей
Приводится определение бесконечно малой последовательности. Она обладает свойствами сходящихся последовательностей. Также имеются свойства, характерные только для последовательностей с пределом равным нулю. Приводятся доказательства таких свойств. Рассмотрен пример, в котором нужно доказать, что последовательность бесконечно малая.
Содержание

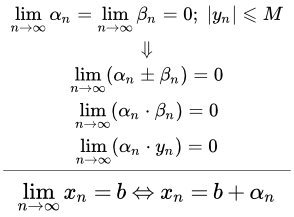
Определение

Бесконечно малая последовательность
{αn} – это сходящаяся последовательность, предел которой равен нулю:
limn → ∞ αn  = 0 .

Согласно определению предела последовательности это означает, что для любого положительного числа ε > 0 существует такое натуральное число N(ε) , зависящее от ε , что для всех натуральных n > N(ε) выполняется неравенство
 | αn  |  < ε .

Свойства бесконечно малых последовательностей

Бесконечно малые последовательности являются сходящимися последовательностями. Поэтому они обладают всеми их свойствами. Формулировки этих свойств и ссылки на страницы с доказательствами приведены на странице
Предел последовательности – основные теоремы и свойства.

Следующие свойства являются прямым следствием арифметических свойств, примененных к последовательностям, предел которых равен нулю.

Сумма и разность бесконечно малых последовательностей
Сумма и разность конечного числа
бесконечно малых последовательностей
является бесконечно малой последовательностью.
Также линейная комбинация конечного числа
бесконечно малых последовательностей
является бесконечно малой последовательностью.
Доказательство
Произведение бесконечно малых последовательностей
Произведение конечного числа
бесконечно малых последовательностей
является бесконечно малой последовательностью.
Доказательство

Следующие свойства относятся только к бесконечно малым последовательностям и не являются прямым следствием свойств сходящихся последовательностей.

Произведение ограниченной последовательности на бесконечно малую
Произведение ограниченной последовательности
на бесконечно малую
является бесконечно малой последовательностью.
Доказательство
Представление сходящейся последовательности через бесконечно малую
Для того, чтобы
последовательность {xn} имела предел b , необходимо и достаточно, чтобы
xn = b + αn ,
где {αn} – бесконечно малая последовательность.
Доказательство

Доказательства свойств

Произведение ограниченной последовательности на бесконечно малую

Все свойства Произведение ограниченной последовательности
на бесконечно малую
является бесконечно малой последовательностью.
Доказательство

Пусть последовательность {xn } ограничена некоторым числом M > 0 :
(3.1)    | xn  |  ≤ M .

Пусть последовательность {αn } – бесконечно малая. То есть имеется такая функция Nα (ε1 ) , зависящая от переменной ε1 , что для любого положительного значения переменной ε1 , выполняется неравенство
(3.2)    | αn  |  < ε1  при  n > Nα (ε1 ) .

Пусть последовательность {yn } является произведением последовательностей {xn } и {αn } . Ее общий член имеет вид:
yn  = xn  ⋅ αn .
Нам нужно найти такую функцию N(ε ) , при которой выполняется неравенство
(3.3)    | yn  |  < ε  при  n > N(ε ) .

Применим (3.1) и (3.2):
 | yn  |  =  | xn  ⋅ αn  |  =  | xn  |  ⋅  | αn  |  < M ⋅ ε1 .
Это выполняется при n > Nα (ε1 ) . Итак,
 | yn  |  < M ⋅ ε1 ;  n > Nα (ε1 ) .
Положим ε1  = ε / M :
 | yn  |  < ε;  n > Nα (ε / M ) .

То есть мы нашли такую функцию N(ε ) = Nα (ε / M ) , при которой, для любого положительного числа ε > 0 , выполняется неравенство:
(3.3)    | yn  |  < ε  при  n > N(ε ) .

Свойство доказано.

Представление сходящейся последовательности через бесконечно малую

Все свойства Для того, чтобы
последовательность {xn} имела предел b , необходимо и достаточно, чтобы
xn = b + αn ,
где {αn} – бесконечно малая последовательность.
Доказательство

Необходимость. Пусть limn → ∞ xn  = b . Рассмотрим последовательность {αn } с общим членом αn  = xn  – b . Используем арифметические свойства пределов:
limn → ∞ αn  = limn → ∞ (xn  – b ) = limn → ∞ xn  – limn → ∞ b = b – b = 0 .
То есть {αn } – бесконечно малая последовательность.

Достаточность. Пусть limn → ∞ αn  = 0 . На основании арифметических свойств пределов имеем:
limn → ∞ xn  = limn → ∞ (b + αn ) = limn → ∞ b + limn → ∞ αn  = b + 0 = b .

Свойство доказано.

Пример

Все примеры Используя определение предела последовательности доказать, что последовательность
αn  = 3n 2  + 2n – 13n 3  – n 2  + 5n – 2
является бесконечно малой.

Решение

Выпишем определение бесконечно малой последовательности:
limn → ∞ αn  = 0  def⇐⇒  ∀ε > 0  ∃Nε   ∀n > Nε  :  | αn  |  < ε .
Поскольку n является натуральным числом, n = 1, 2, 3, ... , то
2n > 1 ,
3n 3  > n 2 ,
5n > 2 .
Поэтому члены последовательности αn являются положительными числами. Тогда
 | αn  |  = αn  = 3n 2  + 2n – 13n 3  – n 2  + 5n – 2 .

Далее замечаем, что
2n ≤ 2n 2 ;
2 ≤ 2n ;
n 2  ≤ n 3 .
Тогда
3n 2  + 2n – 1 < 3n 2  + 2n ≤ 3n 2  + 2n 2  = 5n 2 ;
3n 3  – n 2  + 5n – 2 ≥ 3n 3  – n 3  + 5n – 2n = 2n 3  + 3n > 2n 3 ;
 | αn  |  = 3n 2  + 2n – 13n 3  – n 2  + 5n – 2 < 5n 22n 3 = 52n .

Итак, мы получили следующую оценку:
 | αn  |  < 52n .
Вводим положительные числа ε и Nε :
 | αn  |  < 52n < 52Nε ≤ ε .
Согласно свойствам неравенств, если Nε  ≥ 52ε  и  n > Nε , то
 | αn  |  < ε .

Отсюда следует, что для любого положительного ε > 0 можно найти натуральное число Nε  ≥ 52ε , так что при  n > Nε ,
 | αn  |  < ε .
Это означает, что предел исходной последовательности {αn } равен нулю и, следовательно, она является бесконечно малой.

Ответ

Nε  ≥ 52ε

Автор: Олег Одинцов.     Опубликовано:   Изменено:

▲
Меню