Бесконечно малые и бесконечно большие функции

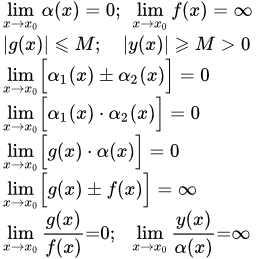
Определения и свойства бесконечно малых и бесконечно больших функций в точке. Связь между ними. Доказательства свойств и теорем. Арифметические свойства пределов с бесконечно малыми и бесконечно большими функциями.

Определение бесконечно малой и бесконечно большой функции

Бесконечно малая функция

Функция α(x) называется бесконечно малой при x стремящемся к x₀, если она имеет равный нулю предел при x → x₀:
.
Здесь x₀ есть конечная или бесконечно удаленная точка: ∞, –∞ или +∞.

Бесконечно большая функция

Функция f(x) называется бесконечно большой при x стремящемся к x₀, если она имеет равный бесконечности предел при x → x₀:
.
Здесь x₀ есть конечная или бесконечно удаленная точка: ∞, –∞ или +∞.

См. также Определение предела функции в точке

Свойства бесконечно малых функций

Свойство суммы, разности и произведения бесконечно малых функций

Сумма, разность и произведение конечного числа бесконечно малых функций при x → x₀ является бесконечно малой функцией при x → x₀.

Это свойство является прямым следствием арифметических свойств пределов функции.

Теорема о произведении ограниченной функции на бесконечно малую

Произведение функции, ограниченной на некоторой проколотой окрестности точки x₀, на бесконечно малую, при x → x₀, является бесконечно малой функцией при x → x₀.
Доказательство ⇓

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Для того, чтобы функция f(x) имела конечный предел , необходимо и достаточно, чтобы
,
где – бесконечно малая функция при x → x₀.
Доказательство ⇓

Свойства бесконечно больших функций

Теорема о сумме ограниченной функции и бесконечно большой

Сумма или разность ограниченной функции, на некоторой проколотой окрестности точки x₀, и бесконечно большой функции, при x → x₀, является бесконечно большой функцией при x → x₀.
Доказательство ⇓

Теорема о произведении ограниченной снизу функции на бесконечно большую

Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция является бесконечно большой при x → x₀:
,
то их произведение является бесконечно большой функцией при :
.
Доказательство ⇓

Теорема о частном от деления ограниченной функции на бесконечно большую

Если функция f(x) → ∞ при x → x₀ (т. е. является бесконечно большой при x → x₀), а функция g(x) – ограничена на некоторой проколотой окрестности точки x₀, то
.
Доказательство ⇓

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция является бесконечно малой при x → x₀:
,
и существует проколотая окрестность точки , на которой  , то
.
Доказательство ⇓

Свойство неравенств бесконечно больших функций

Если функция является бесконечно большой при :
,
и функции и , на некоторой проколотой окрестности точки удовлетворяют неравенству:
,
то функция также бесконечно большая при :
.
Доказательство ⇓

Это свойство имеет два частных случая.

Пусть, на некоторой проколотой окрестности точки , функции и удовлетворяют неравенству:
.
Тогда если , то и .
Если , то и .

Связь между бесконечно большими и бесконечно малыми функциями

Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.

Если функция является бесконечно большой при , то функция является бесконечно малой при .

Если функция являются бесконечно малой при , и , то функция является бесконечно большой при .

Связь между бесконечно малой и бесконечно большой функцией можно выразить символическим образом:
,   .

Если бесконечно малая функция имеет определенный знак при , то есть положительна (или отрицательна) на некоторой проколотой окрестности точки , то можно записать так:
.
Точно также если бесконечно большая функция имеет определенный знак при , то пишут:
,  или  .

Тогда символическую связь между бесконечно малыми и бесконечно большими функциями можно дополнить следующими соотношениями:
,   ,
,   .

Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».

Арифметические свойства бесконечно больших и бесконечно малых функций

Приведенные выше свойства выполняются, если функция ограничена, а функция ограничена снизу по абсолютной величине положительным числом. При этом эти функции не обязательно должны иметь конечный предел, а могут расходиться. Однако, эти функции будут обладать указанными свойствами, если они имеют соответствующие пределы. Это позволяет сформулировать арифметические свойства бесконечно больших и бесконечно малых функций.

Пусть существуют пределы функций
  и   .
И пусть, при , функция является бесконечно малой:
,   а функция – бесконечно большой:
.
Тогда существует пределы суммы и разности:
(A.1)   ;
существуют пределы произведений:
(A.2)   ;
существуют пределы частного:
(A.3)   .

Действительно, если функция имеет конечный предел при , то существует проколотая окрестность , на которой она ограничена (см. «Теорема об ограниченности функции, имеющей конечный предел»).
Если функция имеет не равный нулю предел , то существует проколотая окрестность , на которой она ограничена снизу по абсолютной величине числом :
  при   .
(см. «Теорема об ограниченности снизу функции, имеющей ненулевой предел»).
Тогда, на основе изложенных выше теорем, существуют пределы (А.1 – А.3).

Свойство доказано.

Доказательство свойств и теорем

Теорема о произведении ограниченной функции на бесконечно малую

Все свойства ⇑ Произведение функции , ограниченной на некоторой проколотой окрестности точки x₀:
при ,
на бесконечно малую , при x → x₀:
,
является бесконечно малой функцией при x → x₀:
.

Доказательство

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Все свойства ⇑ Для того, чтобы функция f(x) имела конечный предел , необходимо и достаточно, чтобы
,
где – бесконечно малая функция при x → x₀.

Доказательство

Теорема о сумме ограниченной функции и бесконечно большой

Все свойства ⇑ Сумма или разность ограниченной функции, на некоторой проколотой окрестности точки x₀, и бесконечно большой функции, при x → x₀, является бесконечно большой функцией при x → x₀.

Доказательство

Теорема о произведении ограниченной снизу функции на бесконечно большую

Все свойства ⇑ Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция является бесконечно большой при x → x₀:
,
то их произведение является бесконечно большой функцией при :
.

Доказательство

Теорема о частном от деления ограниченной функции на бесконечно большую

Все свойства ⇑ Если функция f(x) → ∞ при x → x₀ (т. е. является бесконечно большой при x → x₀), а функция g(x) – ограничена на некоторой проколотой окрестности точки x₀, то
.

Доказательство

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Все свойства ⇑ Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция является бесконечно малой при x → x₀:
,
и существует проколотая окрестность точки , на которой  , то
.

Доказательство

Свойство неравенств бесконечно больших функций

Все свойства ⇑ Если функция является бесконечно большой при :
,
и функции и , на некоторой проколотой окрестности точки удовлетворяют неравенству:
,
то функция также бесконечно большая при :
.

Доказательство

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

Автор: Олег Одинцов.     Опубликовано: 14-06-2018   Изменено: 02-02-2020