Число e – его смысл и доказательство сходимости последовательности
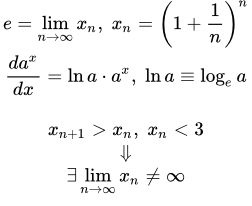
Определение числа e
- Число e
- – это значение предела последовательности:
(1) .
Этот предел является частным случаем второго замечательного предела. Число e иногда называют числом Эйлера или числом Непера. Это самое используемое число в математическом анализе. Оно примерно равно
.
Число e можно представить в виде ряда:
.
Далее приводится объяснение, почему оно так популярно в математике, и дается доказательство существования конечного предела (1).
Смысл числа e
С развитием механики, возникла потребность в вычислении мгновенной скорости движения тел. Для определения скорости v, мы должны взять разность значений координат x в два момента времени и разделить на промежуток времени между ними:
.
По этой формуле, однако, мы не получим мгновенного значения скорости, а получим ее среднее значение в промежутке времени между и . Чтобы найти мгновенную скорость, мы должны положить . Но тогда знаменатель дроби станет равным нулю. Таким образом, эта задача не решается методами классической алгебры.
При попытке решить эту задачу, возникла новая математическая дисциплина – математический анализ. В нем, мгновенная скорость в момент времени t определяется как предел, к которому стремится отношение при , стремящемся к нулю. Этот предел называется производной x по t.
Таким образом, производная является одним из самых важных понятий в математическом анализе. Поэтому необходимо уметь вычислять производные. Оказывается, что если мы найдем производную показательной функции , то ее вычисление сводится к вычислению второго замечательного предела, аналогичного пределу последовательности (1), и выражается через число e:
.
Тогда, если за основание степени a взять число e, то производная будет иметь наиболее простой вид:
.
В связи с этим, в математическом анализе, за основание степени, там где это возможно, выбирают именно число e. Показательная функция с основанием e называется экспонентой. Логарифм по основанию e называется натуральным логарифмом и имеет специальное обозначение . Любую другую показательную функцию (с другим основанием) можно выразить через экспоненту:
.
Таким образом, смысл применения числа e заключается в том, что через него выражается производная показательной функции, и без него просто нельзя обойтись.
Но прежде, чем применять число e, нужно доказать, что оно существует. То есть нужно доказать, что существует конечный предел последовательности при n стремящемся к бесконечности: .
Доказательство сходимости последовательности
Здесь мы покажем, что последовательность с общим членом
(2)
имеет конечный предел. Для этого мы применим теорему Вейерштрасса о пределе монотонной последовательности. Тогда нам нужно доказать, что
1) последовательность (2) монотонна;
2) последовательность (2) ограничена.
Доказательство можно выполнять различными способами.
Применение бинома Ньютона
Рассмотрим последовательность с общим членом
(2) .
Докажем, что она строго возрастает. Для этого применим формулу бинома Ньютона:
Здесь
– биноминальные коэффициенты.
Подставим и выполним преобразования. Тогда элемент запишется в виде суммы положительных членов:
.
Выполняя деление в каждом члене на , имеем:
(3)
Для элемента имеем сумму положительных членов:
Далее замечаем, что
Таким образом, каждый член в , начиная с третьего по n + 1-ый, больше соответствующего члена в . Кроме этого, в на один положительный член больше. Поэтому
То есть последовательность строго возрастает.
Докажем, что эта последовательность ограничена. Поскольку она возрастает, то снизу она ограниченна значением . Докажем, что последовательность ограничена сверху. Для этого замечаем, что
Тогда
Далее замечаем, что . Тогда
.
Применим формулу суммы членов геометрической прогрессии:
.
Отсюда получаем ограниченность :
.
Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.
Применение неравенства Бернулли
Снова рассматриваем последовательность
(2) .
Докажем ее монотонность и ограниченность применяя неравенство Бернулли. При и при натуральном , имеет место следующее неравенство:
(4) .
Докажем с его помощью, что последовательность строго возрастает. Выпишем ее элементы в следующем виде:
, .
Тогда
.
Преобразуем второй множитель и применим неравенство Бернулли:
;
.
Поскольку , то строгое возрастание последовательности доказано.
Докажем, что последовательность ограничена. Поскольку она возрастает, то нам нужно доказать ее ограниченность сверху. Для четных n, является натуральным числом. Имеем:
;
.
Отсюда следует, что элементы последовательности с четными номерами ограничены:
.
Если n нечетно, то используем тот факт, что последовательность строго возрастает. Тогда четно. Поэтому и при нечетных n, элементы последовательности ограничены:
.
Итак, мы показали, что последовательность монотонна и ограничена. Тогда по теореме Вейерштрасса, она имеет конечный предел.
Использование вспомогательной последовательности
Для исследования сходимости исходной последовательности, иногда бывает удобно взять вспомогательную последовательность, которую легче исследовать. При этом предел исходной последовательности должен выражаться через предел вспомогательной.
В нашем случае, для исследования сходимости последовательности
(2) ,
возьмем вспомогательную последовательность
(5) .
Покажем, что она строго убывает. Для этого используем неравенство Бернулли:
(4) .
Имеем:
;
.
Поскольку , то отсюда следует, что последовательность строго убывает.
Покажем, что ограничена. Поскольку она убывает, то сверху она ограничена значением . Покажем, что последовательность ограничена снизу. Снова применяем неравенство Бернулли:
;
.
Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.
Элементы исходной последовательности выражаются через :
.
Далее замечаем, что
.
Применяем теорему о пределе частного числовой последовательности:
.
Поскольку последовательность имеет конечный предел, то и исходная последовательность имеет конечный предел.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
