Теорема Вейерштрасса о пределе монотонной последовательности
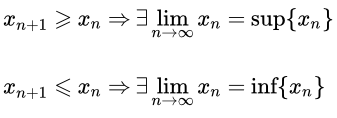
Теорема Вейерштрасса о пределе монотонной последовательности
Пусть {xn} – монотонная ограниченная последовательность.Тогда она имеет конечный предел, равный точной верней границе, sup {xn} для неубывающей и точной нижней границе, inf {xn} для невозрастающей последовательности.
Пусть {xn} – монотонная неограниченная последовательность.
Тогда она имеет бесконечный предел, равный плюс бесконечности, + ∞ для неубывающей и минус бесконечности, – ∞ для невозрастающей последовательности.
Доказательство
Ограниченная неубывающая последовательность
1) Пусть последовательность {xn } является неубывающей ограниченной последовательностью.
Поскольку последовательность неубывающая, то для всех n выполняются неравенства:
(1.1) xn + 1 ≥ xn .
Поскольку последовательность ограничена, то она имеет конечную точную верхнюю границу
a = sup {xn } .
Это означает, что:
- для всех n ,
(1.2) xn ≤ a ;
- для любого положительного числа ε > 0 , существует такой номер N = N(ε ) , зависящий от ε , так что
(1.3) xN > a – ε .
Поскольку последовательность {xn } неубывающая, то при n > N имеем:
xn ≥ xN > a – ε .
Здесь мы также использовали (1.3). Комбинируя с (1.2), находим:
a – ε < xn ≤ a при n > N .
Поскольку a < a + ε , то
a – ε < xn < a + ε ,
или
| xn – a | < ε при n > N .
Это и означает, что число a = sup {xn } является пределом последовательности {xn } .
Первая часть теоремы доказана.
Ограниченная невозрастающая последовательность
2) Пусть теперь последовательность {xn } является невозрастающей ограниченной последовательностью:
(2.1) xn + 1 ≤ xn для всех n .
Поскольку последовательность ограничена, то она имеет конечную точную нижнюю границу
a = inf {xn } .
Это означает следующее:
- для всех n выполняются неравенства:
(2.2) xn ≥ a ;
- для любого положительного числа ε > 0 , существует такой номер N = N(ε ) , зависящий от ε , для которого
(2.3) xN < a + ε .
Поскольку последовательность {xn } невозрастающая, то при n > N имеем:
xn ≤ xN < a + ε .
Здесь мы также использовали (2.3). Учитывая (2.2), находим:
a ≤ xn < a + ε при n > N .
Поскольку a > a – ε , то
a – ε < xn < a + ε ,
или
| xn – a | < ε при n > N .
Это и означает, что число a = inf {xn } является пределом последовательности {xn } .
Вторая часть теоремы доказана.
Неограниченная неубывающая последовательность
Теперь рассмотрим неограниченные последовательности.
3) Пусть последовательность {xn } является неограниченной неубывающей последовательностью.
Поскольку последовательность неубывающая, то для всех n выполняются неравенства:
(3.1) xn + 1 ≥ xn .
Поскольку последовательность является неубывающей и неограниченной, то она неограниченна с правой стороны. Тогда для любого числа M существует такой номер N = N(M ) , зависящий от M , для которого
(3.2) xN > M .
Поскольку последовательность {xn } неубывающая, то при n > N имеем:
xn ≥ xN > M .
Здесь мы также использовали (3.2).
Итак, для любого числа M существует такое натуральное число N = N(M ) , зависящее от M , так что для всех номеров n > N выполняются неравенства:
xn > M .
Это означает, что предел последовательности {xn } равен плюс бесконечности:
limn → ∞ xn = + ∞ .
Третья часть теоремы доказана.
Неограниченная невозрастающая последовательность
4) Наконец рассмотрим случай, когда {xn } является неограниченной невозрастающей последовательностью.
Аналогично предыдущему, поскольку последовательность невозрастающая, то
(4.1) xn + 1 ≤ xn для всех n .
Поскольку последовательность является невозрастающей и неограниченной, то она неограниченна с левой стороны. Тогда для любого числа M существует такой номер N = N(M ) , зависящий от M , для которого
(4.2) xN < – M .
Поскольку последовательность {xn } невозрастающая, то при n > N имеем:
xn ≤ xN < – M .
Итак, для любого числа M существует такое натуральное число N = N(M ) , зависящее от M , так что для всех номеров n > N выполняются неравенства:
xn < – M .
Это означает, что предел последовательности {xn } равен минус бесконечности:
limn → ∞ xn = – ∞ .
Теорема доказана.
Пример решения задачи
Все примеры Пользуясь теоремой Вейерштрасса, доказать сходимость последовательности:
x1 = √ 12 , x2 = √ 12 + √ 12 , . . . , xn = √ 12 + √ 12 + ... + √ 12 n корней , . . .
После чего найти ее предел.
Решение
Представим последовательность в виде рекуррентных формул:
x1 = √ 12 ,
xn + 1 = √ 12 + xn .
Докажем, что заданная последовательность ограничена сверху значением
(П1) xn < 4 .
Доказательство выполняем методом математической индукции.
x1 = √ 12 < √ 16 = 4 .
Пусть xn < 4 . Тогда
xn + 1 = √ 12 + xn < √ 12 + 4 = 4 .
Неравенство (П1) доказано.
Докажем, что последовательность монотонно возрастает.
xn + 1 – xn = x 2n + 1 – x 2nxn + 1 + xn = 12 + xn – x 2nxn + 1 + xn = (3 + xn )(4 – xn )xn + 1 + xn ;
(П2) xn + 1 – xn = (3 + xn )(4 – xn )xn + 1 + xn .
Поскольку xn > 0 , то знаменатель дроби и первый множитель в числителе положительные. В силу ограниченности членов последовательности неравенством (П1), второй множитель также положителен. Поэтому
xn + 1 – xn > 0 .
То есть последовательность является строго возрастающей.
Поскольку последовательность возрастает и ограничена сверху, то она является ограниченной последовательностью. Поэтому, по теореме Вейерштрасса, она имеет предел.
Найдем этот предел. Обозначим его через a :
limn → ∞ xn = a .
Воспользуемся тем, что
limn → ∞ (xn + 1 – xn ) = 0 .
Применим это к (П2), используя арифметические свойства пределов сходящихся последовательностей:
(3 + a )(4 – a )a + a = 0 .
Условию xn > 0 удовлетворяет корень a = 4 .
Ответ
limn → ∞ xn = 4 .
Автор: Олег Одинцов. Опубликовано: