Справочные данные по гиперболическим функциям – свойства, графики, формулы
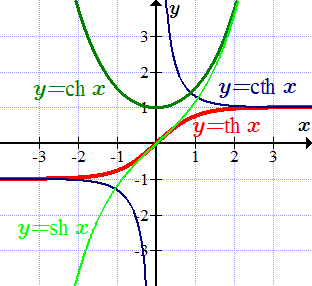
Определения гиперболических функций, их области определений и значений
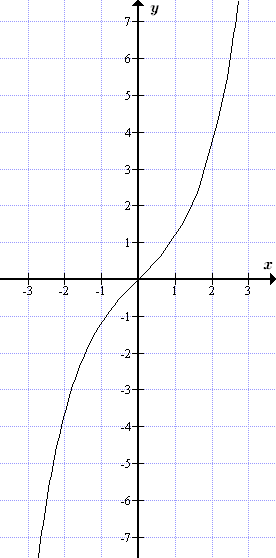
- sh x – гиперболический синус
- , –∞ < x < +∞; –∞ < y < +∞.
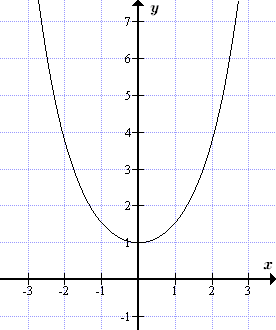
- ch x – гиперболический косинус
- , –∞ < x < +∞; 1 ≤ y < +∞.
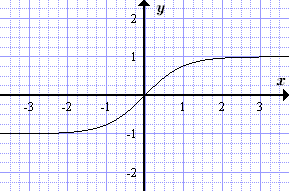
- th x – гиперболический тангенс
- , –∞ < x < +∞; – 1 < y < +1.
- cth x – гиперболический котангенс
- , x ≠ 0; y < –1 или y > +1.
Графики гиперболических функций
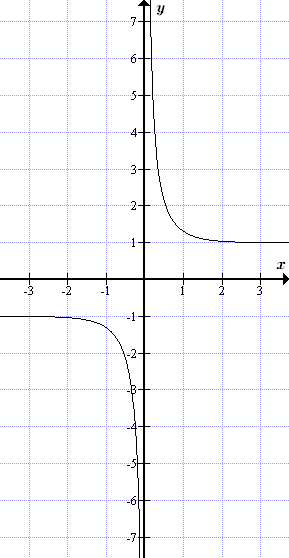
Формулы с гиперболическими функциями
Связь с тригонометрическими функциями
sin iz = i sh z ; cos iz = ch z
sh iz = i sin z ; ch iz = cos z
tg iz = i th z ; ctg iz = – i cth z
th iz = i tg z ; cth iz = – i ctg z
Здесь i – мнимая единица, i2 = –1.
Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.
Четность
sh(–x) = – sh x; ch(–x) = ch x.
th(–x) = – th x; cth(–x) = – cth x.
Функция ch(x) – четная. Функции sh(x), th(x), cth(x) – нечетные.
Разность квадратов
ch2 x – sh2 x = 1.
Формулы суммы и разности аргументов
sh(x ± y) = sh x ch y ± ch x sh y,
ch(x ± y) = ch x ch y ± sh x sh y,
,
,
sh 2x = 2 sh x ch x ,
ch 2x = ch2 x + sh2 x = 2 ch2 x – 1 = 1 + 2 sh2 x,
.
Формулы произведений гиперболического синуса и косинуса
,
,
,
,
,
.
Формулы суммы и разности гиперболических функций
,
,
,
,
.
Связь гиперболического синуса и косинуса с тангенсом и котангенсом
, ,
, .
Производные
,
Интегралы от sh x, ch x, th x, cth x
,
,
.
Разложения в ряды
.
,
,
.
Обратные функции
Ареасинус
При – ∞ < x < ∞ и – ∞ < y < ∞ имеют место формулы:
,
.
Ареакосинус
При 1 ≤ x < ∞ и 0 ≤ y < ∞ имеют место формулы:
,
.
Вторая ветвь ареакосинуса расположена при 1 ≤ x < ∞ и – ∞ < y ≤ 0 :
.
Ареатангенс
При – 1 < x < 1 и – ∞ < y < ∞ имеют место формулы:
,
.
Ареакотангенс
При – ∞ < x < – 1 или 1 < x < ∞ и y ≠ 0 имеют место формулы:
,
.
Автор: Олег Одинцов. Опубликовано:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
