Примеры решений кубических уравнений
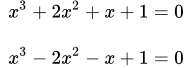
Обзор методов решения кубических уравнений приведен на странице “Решение кубических уравнений”. Здесь мы приводим два примера, используя формулы Кардано и Виета.
Пример решения кубического уравнения с комплексными корнями
Решить кубическое уравнение:
(1.1) .
Решение
Поиск целых корней
Уравнение (1.1) имеет целые коэффициенты. Проверим, не содержит ли это уравнение целых корней. Член без – это 1. У числа 1 есть два делителя: 1 и – 1. Подставим в уравнение (1.1) и . Ни для одного из этих чисел уравнение не выполняется. Следовательно, целых корней нет.
Сведение уравнения к приведенному виду
Пусть обозначают коэффициенты при , и свободный член. Делаем подстановку
(1.2) .
В результате получаем уравнение приведенного вида:
(1.3) ,
где
;
.
Определение вида корней
Определяем, имеет ли уравнение комплексные корни. Для этого находим дискриминант:
.
Дискриминант положителен. Следовательно, уравнение имеет один действительный корень и два комплексно сопряженных.
Нахождение корней по формуле Кардано
Поскольку дискриминант положителен, то находим корни по формуле Кардано:
, ,
где
; ; .
При , для величин и , можно взять действительные значения корней. Тогда соотношение выполняется автоматически.
В нашем случае:
;
;
;
;
;
;
;
;
.
Итак, мы нашли корни неполного кубического уравнения. По формуле (1.2) находим корни исходного уравнения:
.
Ответ
;
;
.
Пример с действительными корнями
Решить кубическое уравнение:
(2.1) .
Решение
Поиск целых корней
Уравнение (2.1) имеет целые коэффициенты. Проверим, нет ли у этого уравнения целых корней. Свободный член – это 1. У него есть два делителя: 1 и – 1. Подставим в уравнение (2.1) и . Уравнение не выполняется ни для одного из этих чисел. Следовательно, целых корней нет.
Сведение уравнения к приведенному виду
В исходном уравнении (2.1),
.
Делаем подстановку
(2.2)
и приводим уравнение (2.1) к приведенному (неполному) виду:
(2.3) ,
где
;
.
Определение вида корней
Определяем, имеет ли уравнение комплексные корни. Находим дискриминант:
.
Дискриминант отрицателен. Следовательно, уравнение имеет три действительных корня.
Нахождение корней по формуле Виета
Поскольку дискриминант отрицателен, то находим корни по формуле Виета:
;
;
;
;
.
Итак, мы нашли корни приведенного кубического уравнения. По формуле (2.2) находим корни исходного уравнения:
.
Ответ
;
;
.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.
Автор: Олег Одинцов. Опубликовано:
