Теорема о двух милиционерах
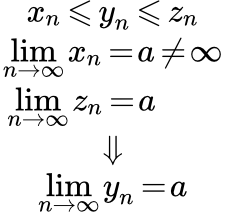
Теорема о промежуточной последовательности
Пусть последовательности {xn} и {zn} сходятся к одному конечному числу a: . И пусть элементы последовательности {yn}, начиная с некоторого номера, удовлетворяют неравенствам xn ≤ yn ≤ zn. То есть они находятся в промежутке между элементами последовательностей {xn} и {zn}. Тогда эта последовательность также сходится к числу a: .
Эта теорема также выполняется, если a есть бесконечно удаленная точка определенного знака: или . Но она не справедлива, если . См. «Свойство неравенств бесконечно больших последовательностей».
Математики тоже шутят. Поэтому эту теорему иногда называют Теоремой о двух милиционерах (полицейских). Также, эту теорему иногда называют леммой, и она имеет другие названия: теорема (лемма) о зажатой последовательности, теорема о трех последовательностях, теорема о пределе промежуточной последовательности.
Теорема о двух милиционерах
Если два милиционера {xn} и {zn} идут в милицейский участок a: , то оказавшийся между ними подозреваемый {yn}, xn ≤ yn ≤ zn, также придет в этот участок:
.
Доказательство
Поскольку существуют конечные пределы и , то, согласно определению предела последовательности, имеются функции и такие, что для любого положительного числа ε > 0 выполняются следующие неравенства:
при ;
при .
По условию, имеется некоторое число n0. Так что при выполняются неравенства:
.
Выберем произвольное положительное значение переменной ε. Пусть означает наибольшее из чисел , и . Тогда при выполняются следующие неравенства:
(4.1) ;
(4.2) ;
(4.3) .
Из (4.1) и (4.2) следует, что
;
.
Учитывая (4.3), имеем:
;
.
Отсюда
.
Или
.
Итак, мы нашли такую функцию , при которой, для любого положительного числа , выполняются неравенства:
.
Это означает, что последовательность имеет предел и он равен a:
.
Теорема доказана.
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов с помощью теоремы о двух милиционерах.
⇓ ⇓
Пример 1
Все примеры ⇑ Используя значение предела , найти предел последовательности при .
Решение
Используем то, что функция синус ограничена:
.
Разделим эти неравенства на положительное число n. Поскольку , то неравенства не меняют знаки:
(П1.1) .
Рассмотрим последовательности с элементами и . Их пределы известны:
;
.
Согласно (П1.1), элементы последовательности заключены между элементами и :
.
Тогда, на основании теоремы о двух милиционерах:
.
Ответ
.
Пример 2
Все примеры ⇑ Найти предел последовательности при , используя теорему о двух милиционерах.
Решение
Воспользуемся свойствами показательной функции:
.
Чтобы избежать громоздких формул, введем обозначение:
.
Тогда .
Преобразуем элемент заданной последовательности в следующем виде:
.
Поскольку , то убывает с ростом n. Номер элемента n принимает только натуральные значения . Поэтому
.
Кроме этого, согласно свойствам показательной функции,
.
Таким образом,
.
Разделим эти неравенства на положительное число n. Поскольку , то неравенства не меняют знаки:
(П2.1) .
Далее заметим, что если выполняется строгое неравенство , то автоматически выполняется нестрогое: . Поэтому мы можем заменить в (П2.1) знак строгого неравенства на знак нестрогого:
(П2.2) .
Далее, вводим последовательность x_n, состоящую из постоянных элементов, равных нулю:
.
Согласно свойству таких последовательностей, она имеет предел:
.
Вводим последовательность . Воспользуемся тем, что . Применяя арифметические свойства пределов последовательностей, находим:
.
Из (П2.2) мы видим, что элементы последовательности зажаты между элементами и :
.
Поскольку , то по теореме о зажатой последовательности, .
Ответ
.
Автор: Олег Одинцов. Опубликовано:
