Экспонента, е в степени х
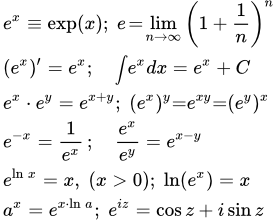
Определение
- Экспонента
- – это показательная функция y(x) = e x, производная которой равна самой функции.
Экспоненту обозначают так , или .
Число e
Основанием степени экспоненты является число e. Это иррациональное число. Оно примерно равно
е ≈ 2,718281828459045...
Число e определяется через предел последовательности. Это, так называемый, второй замечательный предел:
.
Также число e можно представить в виде ряда:
.
График экспоненты
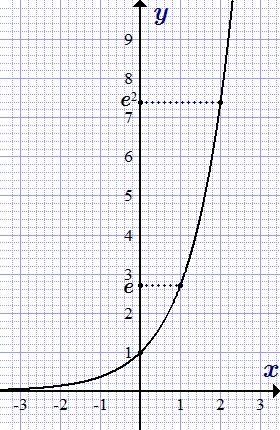
На графике представлена экспонента, е в степени х.
y(x) = е х
На графике видно, что экспонента монотонно возрастает.
Формулы
Основные формулы такие же, как и для показательной функции с основанием степени е.
;
;
;
.
Выражение показательной функции с произвольным основанием степени a через экспоненту:
.
См. также раздел "Показательная функция" >>>
Частные значения
Пусть y(x) = e x. Тогда
.
Свойства экспоненты
Экспонента обладает свойствами показательной функции с основанием степени е > 1.
Область определения, множество значений
Экспонента y(x) = e x определена для всех x.
Ее область определения:
– ∞ < x + ∞.
Ее множество значений:
0 < y < + ∞.
Экстремумы, возрастание, убывание
Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = е х | |
| Область определения | – ∞ < x < + ∞ |
| Область значений | 0 < y < + ∞ |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 |
| + ∞ | |
| 0 |
Обратная функция
Обратной для экспоненты является натуральный логарифм.
;
.
Производная экспоненты
Производная е в степени х равна е в степени х:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
См. также раздел "Таблица неопределенных интегралов" >>>
Комплексные числа
Действия с комплексными числами осуществляются при помощи формулы Эйлера:
,
где есть мнимая единица:
.
Выражения через гиперболические функции
; ;
.
Выражения через тригонометрические функции
; ;
;
.
Разложение в степенной ряд
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
