Обратные тригонометрические функции, их графики и формулы
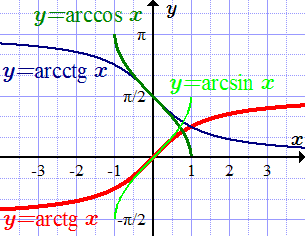
Определение обратных тригонометрических функций
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x , при заданном y (– 1 ≤ y ≤ 1 ) , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x . Если ограничить аргумент x интервалом – π2 ≤ x ≤ π2 , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y .
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
- Арксинус ( y = arcsin x )
- – это функция, обратная к синусу ( x = sin y ), имеющая область определения – 1 ≤ x ≤ 1 и множество значений – π2 ≤ y ≤ π2 .
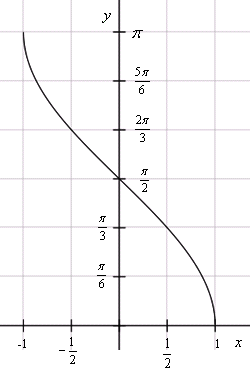
- Арккосинус ( y = arccos x )
- – это функция, обратная к косинусу ( x = cos y ), имеющая область определения – 1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π .
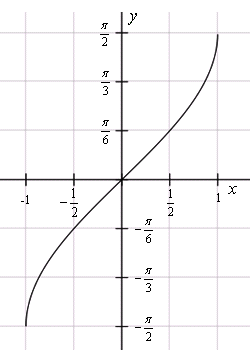
- Арктангенс ( y = arctg x )
- – это функция, обратная к тангенсу ( x = tg y ), имеющая область определения – ∞ < x < + ∞ и множество значений – π2 < y < π2 .
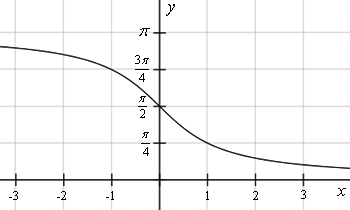
- Арккотангенс ( y = arcctg x )
- – это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения – ∞ < x < + ∞ и множество значений 0 < y < π .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус, Тангенс, котангенс.
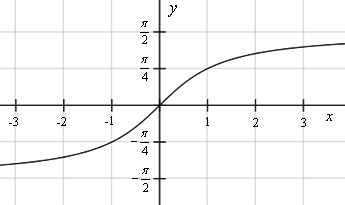
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x) = x при – π2 ≤ x ≤ π2
sin(arcsin x) = x
arccos(cos x) = x при 0 ≤ x ≤ π
cos(arccos x) = x
arctg(tg x) = x при – π2 < x < π2
tg(arctg x) = x
arcctg(ctg x) = x при 0 < x < π
ctg(arcctg x) = x
Формулы, связывающие обратные тригонометрические функции
См. Вывод формул обратных тригонометрических функций
arcsin x = – arcsin (– x ) = π2 – arccos x = arctg x√ 1 – x 2
arccos x = π – arccos (– x ) = π2 – arcsin x = arcctg x√ 1 – x 2
arctg x = – arctg (– x ) = π2 – arcctg x = arcsin x√ 1 + x 2
arcctg x = π – arcctg (– x ) = π2 – arctg x = arccos x√ 1 + x 2
Формулы суммы и разности
arcsin x + arcsin y = arcsin ( x √ 1 – y 2 + y √ 1 – x 2 )
при xy ≤ 0 или x 2 + y 2 ≤ 1
arcsin x + arcsin y = π – arcsin ( x √ 1 – y 2 + y √ 1 – x 2 )
при x > 0, y > 0 и x 2 + y 2 > 1
arcsin x + arcsin y = – π – arcsin ( x √ 1 – y 2 + y √ 1 – x 2 )
при x < 0, y < 0 и x 2 + y 2 > 1
arcsin x – arcsin y = arcsin ( x √ 1 – y 2 – y √ 1 – x 2 )
при xy ≥ 0 или x 2 + y 2 ≤ 1
arcsin x – arcsin y = π – arcsin ( x √ 1 – y 2 – y √ 1 – x 2 )
при x > 0, y < 0 и x 2 + y 2 > 1
arcsin x – arcsin y = – π – arcsin ( x √ 1 – y 2 – y √ 1 – x 2 )
при x < 0, y > 0 и x 2 + y 2 > 1
arccos x + arccos y = arccos ( xy – √ 1 – x 2 √ 1 – y 2 )
при x + y ≥ 0
arccos x + arccos y = 2π – arccos ( xy – √ 1 – x 2 √ 1 – y 2 )
при x + y < 0
arccos x – arccos y = – arccos ( xy + √ 1 – x 2 √ 1 – y 2 )
при x ≥ y
arccos x – arccos y = arccos ( xy + √ 1 – x 2 √ 1 – y 2 )
при x < y
arctg x + arctg y = arctg x + y1 – xy
при xy < 1
arctg x + arctg y = π + arctg x + y1 – xy
при x > 0, xy > 1
arctg x + arctg y = – π + arctg x + y1 – xy
при x < 0, xy > 1
arctg x – arctg y = arctg x – y1 + xy
при xy > – 1
arctg x – arctg y = π + arctg x – y1 + xy
при x > 0, xy < – 1
arctg x – arctg y = – π + arctg x – y1 + xy
при x < 0, xy < – 1
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: