Элементарные функции в картинках
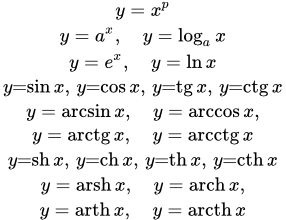
Приводятся основные сведения по элементарным функциям в сжатом виде – в виде картинок со ссылками на страницы с подробным изложением.
Здесь приводятся главные картинки раздела «Справочник по элементарным функциям». На этих изображениях, в кратком виде представлены главные содержания страниц раздела. У каждого изображения имеется заголовок и ссылка на страницу, к которой относится картинка.
Степенная функция и корни - определение, свойства и формулы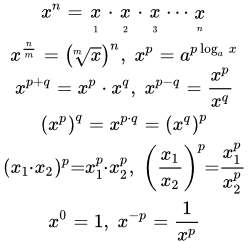 Приведены основные свойства степенной функции, включая формулы и свойства корней. Представлены производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел степенной функции.
Приведены основные свойства степенной функции, включая формулы и свойства корней. Представлены производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел степенной функции. 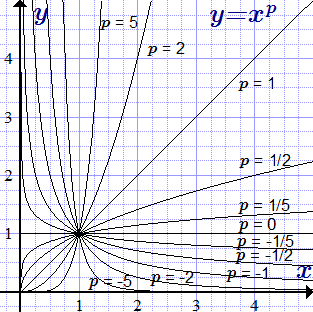 Графики степенной функции y = x p при различных значениях показателя p. Степенная функция, ее свойства и графики
Графики степенной функции y = x p при различных значениях показателя p. Степенная функция, ее свойства и графики Представлены свойства и графики степенных функций при различных значениях показателя степени. Основные формулы, области определения и множества значений, четность, монотонность, возрастание и убывание, экстремумы, выпуклость, перегибы, точки пересечения с осями координат, пределы, частные значения.
Представлены свойства и графики степенных функций при различных значениях показателя степени. Основные формулы, области определения и множества значений, четность, монотонность, возрастание и убывание, экстремумы, выпуклость, перегибы, точки пересечения с осями координат, пределы, частные значения. 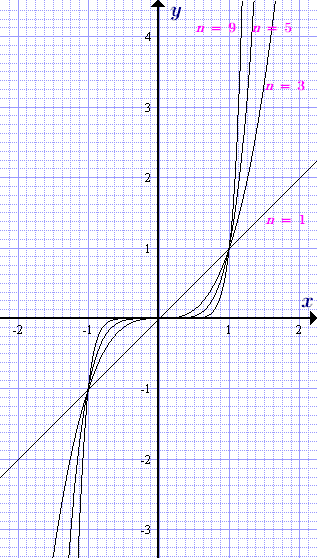 Графики степенной функции y = xn с натуральным нечетным показателем n = 1, 3, 5, ....
Графики степенной функции y = xn с натуральным нечетным показателем n = 1, 3, 5, .... 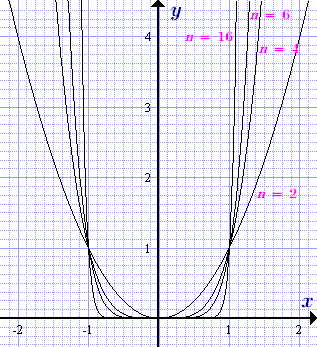 Графики степенной функции y = xn с натуральным четным показателем n = 2, 4, 6, ....
Графики степенной функции y = xn с натуральным четным показателем n = 2, 4, 6, .... 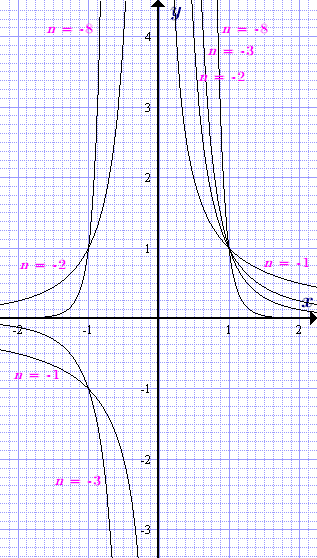 Графики степенной функции y = xn с целым отрицательным показателем n = -1, -2, -3, ....
Графики степенной функции y = xn с целым отрицательным показателем n = -1, -2, -3, .... 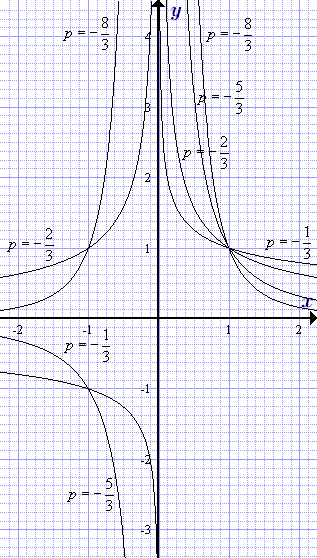 Графикии степенных функций y = xp = xn/m с рациональным отрицательным показателем p = n/m, где m = 3, 5, 7, ... - нечетное.
Графикии степенных функций y = xp = xn/m с рациональным отрицательным показателем p = n/m, где m = 3, 5, 7, ... - нечетное. 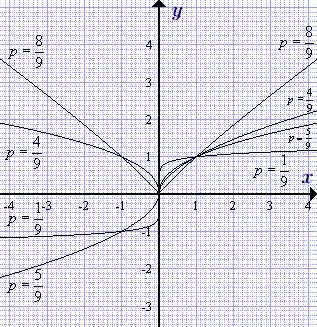 Графики степенной функции y = xp = xn/m с рациональным показателем p = n/m, где m = 3, 5, 7, ... - нечетное, 0 < p < 1.
Графики степенной функции y = xp = xn/m с рациональным показателем p = n/m, где m = 3, 5, 7, ... - нечетное, 0 < p < 1. 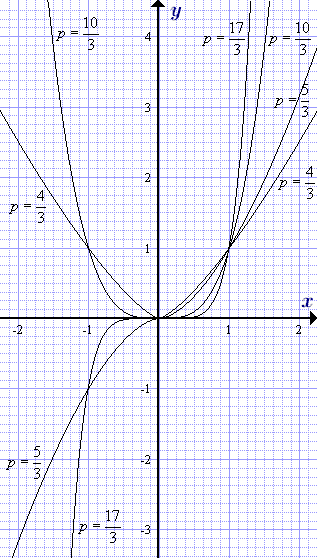 Графики степенной функции y = xp = xn/m с рациональным показателем p = n/m, где m = 3, 5, 7, ... - нечетное, p > 1. Показательная функция – свойства, графики, формулы
Графики степенной функции y = xp = xn/m с рациональным показателем p = n/m, где m = 3, 5, 7, ... - нечетное, p > 1. Показательная функция – свойства, графики, формулы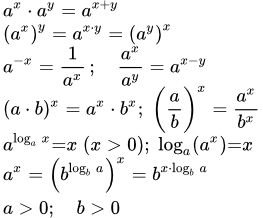 Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел. 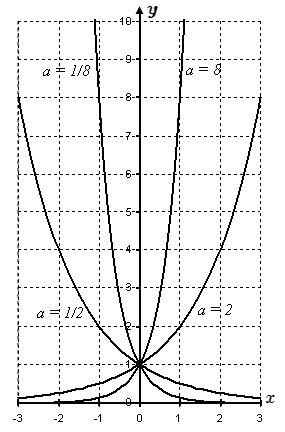 Графики показательной функции y = ax при различных значениях основания a. Логарифм - свойства, формулы, график
Графики показательной функции y = ax при различных значениях основания a. Логарифм - свойства, формулы, график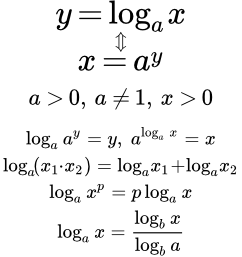 Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел. 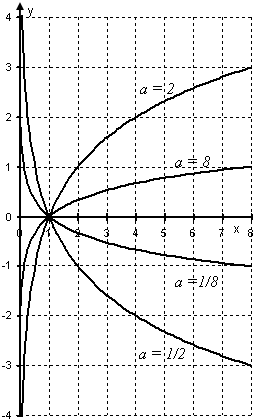 Графики логарифма y = loga x при различных значениях основания a. Экспонента, е в степени х
Графики логарифма y = loga x при различных значениях основания a. Экспонента, е в степени х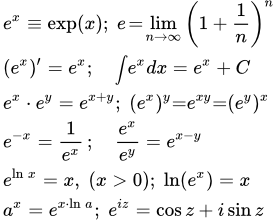 Приведены график и основные свойства экспоненты (е в степени х): область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд, действия с комплексными числами.
Приведены график и основные свойства экспоненты (е в степени х): область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд, действия с комплексными числами. 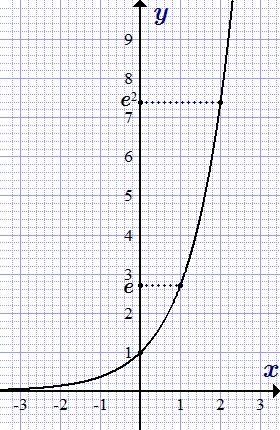 График экспоненты, y = ex. Натуральный логарифм, функция ln x
График экспоненты, y = ex. Натуральный логарифм, функция ln x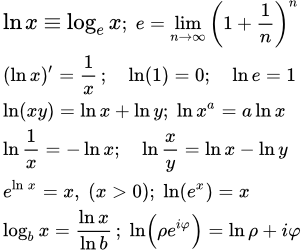 Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел. 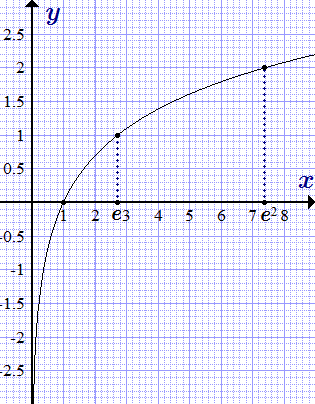 График функции y = ln x. Синус (sin x) и косинус (cos x) – свойства, графики, формулы
График функции y = ln x. Синус (sin x) и косинус (cos x) – свойства, графики, формулы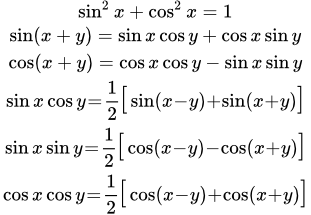 Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями. 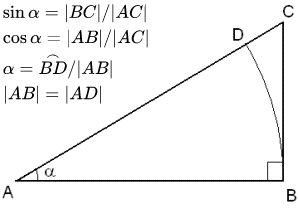 Геометрическое определение синуса и косинуса
Геометрическое определение синуса и косинуса 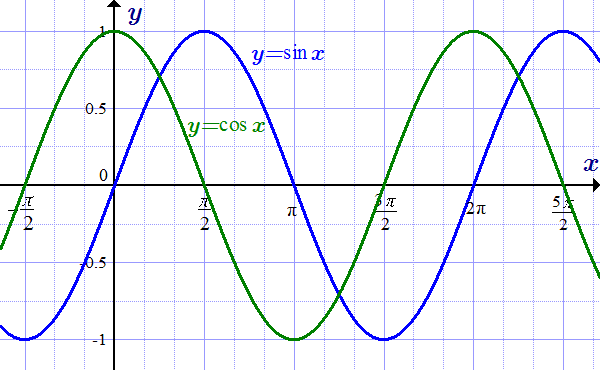 Графики функций y=sin(x) и y=cos(x).
Графики функций y=sin(x) и y=cos(x). 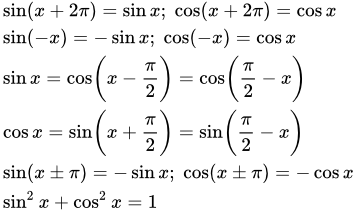 Периодичность, четность и основные формулы синуса и косинуса
Периодичность, четность и основные формулы синуса и косинуса 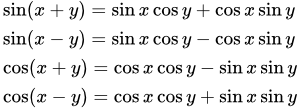 Формулы синуса и косинуса от суммы и разности аргументов
Формулы синуса и косинуса от суммы и разности аргументов 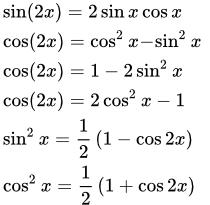 Синус и косинуса двойного угла.
Синус и косинуса двойного угла. 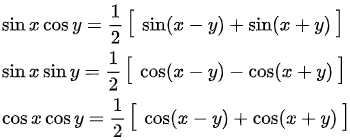 Формулы произведения синусов и косинусов
Формулы произведения синусов и косинусов 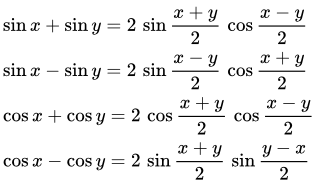 Формулы суммы и разности синуса и косинуса
Формулы суммы и разности синуса и косинуса 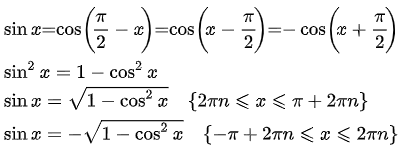 Выражение синуса через косинус
Выражение синуса через косинус 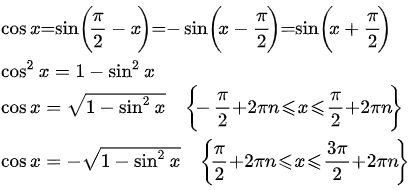 Выражение косинуса через синус
Выражение косинуса через синус 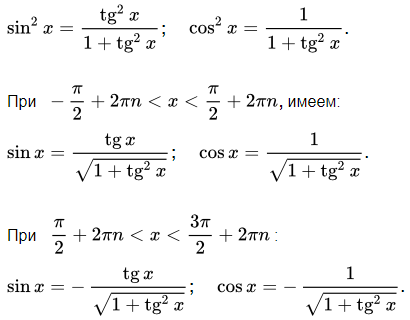 Выражение синуса и косинуса через тангенс
Выражение синуса и косинуса через тангенс 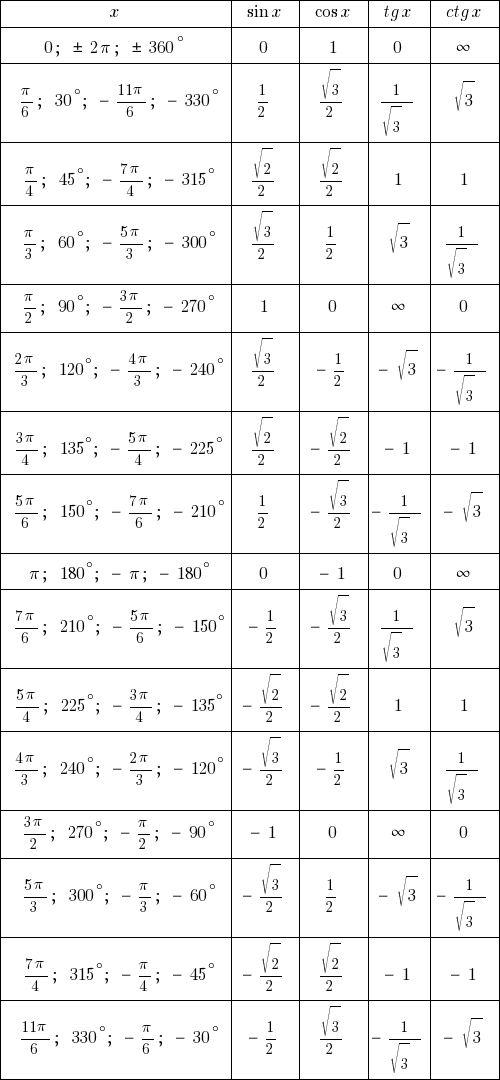 Таблица синусов и косинусов Тангенс (tg x) и котангенс (ctg x) – свойства, графики, формулы
Таблица синусов и косинусов Тангенс (tg x) и котангенс (ctg x) – свойства, графики, формулы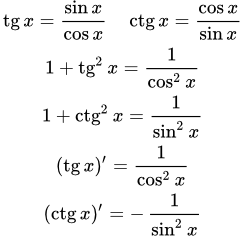 Справочные данные по тангенсу (tg x) и котангенсу (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица тангенсов и котангенсов, производные, интегралы, разложения в ряды. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Справочные данные по тангенсу (tg x) и котангенсу (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица тангенсов и котангенсов, производные, интегралы, разложения в ряды. Выражения через комплексные переменные. Связь с гиперболическими функциями. 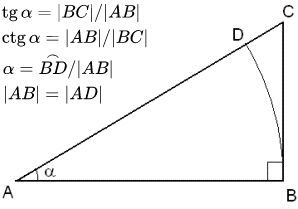 Геометрическое определение тангенса и котангенса
Геометрическое определение тангенса и котангенса 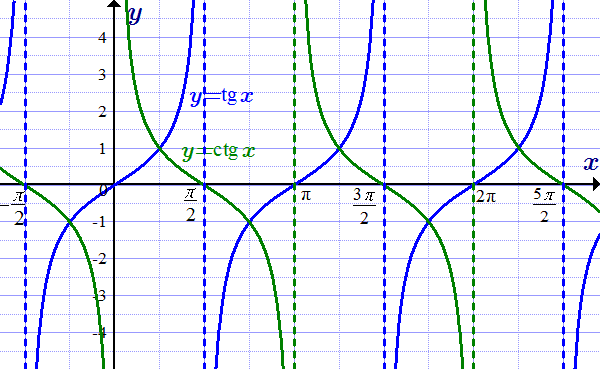 Графики функций y=tg(x) и y=ctg(x).
Графики функций y=tg(x) и y=ctg(x). 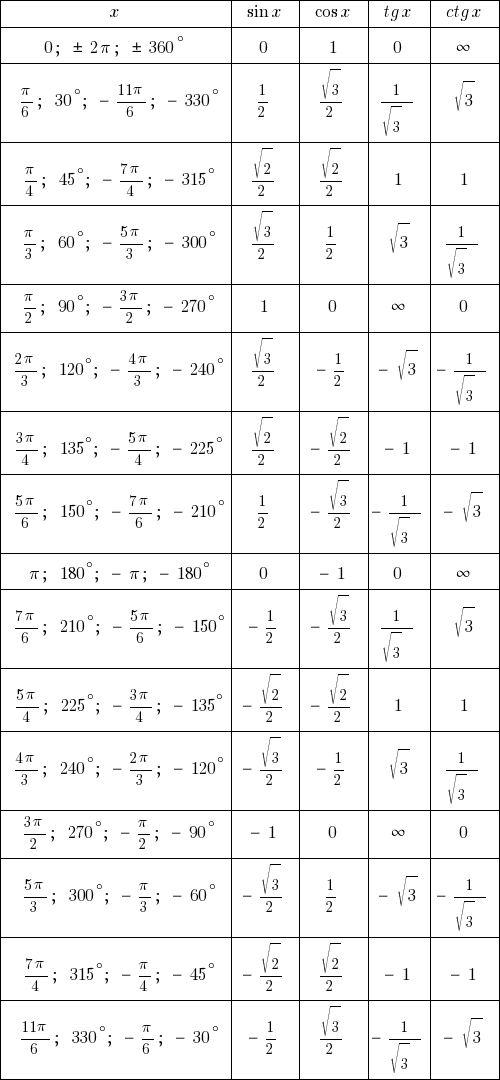 Таблица тангенсов и котангенсов Обратные тригонометрические функции, их графики и формулы
Таблица тангенсов и котангенсов Обратные тригонометрические функции, их графики и формулы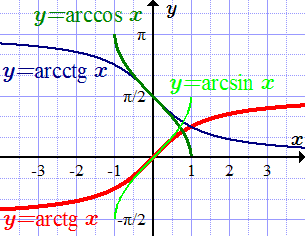 Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.
Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей. 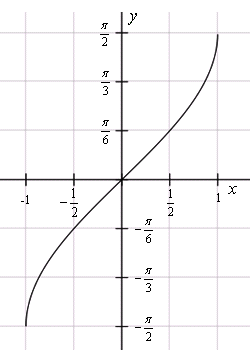 y = arcsin x
y = arcsin x 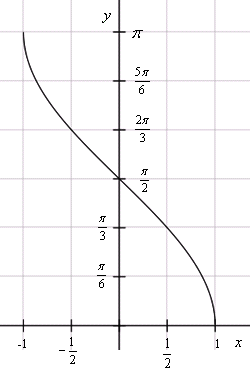 y = arccos x
y = arccos x 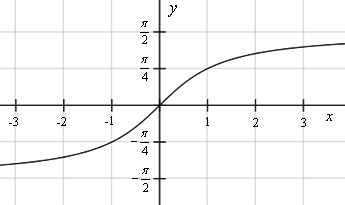 y = arctg x
y = arctg x 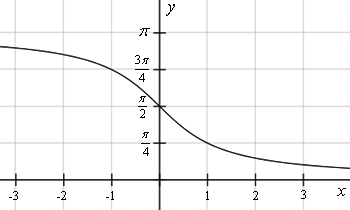 y = arcctg x Арксинус, арккосинус - свойства, графики, формулы
y = arcctg x Арксинус, арккосинус - свойства, графики, формулы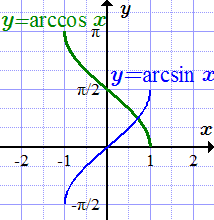 Даны свойства арксинуса и арккосинуса, их графики, формулы, таблица арксинусов и арккосинусов. Выражения через комплексные числа, гиперболические функции. Производные, интегралы, разложение в степенной ряд.
Даны свойства арксинуса и арккосинуса, их графики, формулы, таблица арксинусов и арккосинусов. Выражения через комплексные числа, гиперболические функции. Производные, интегралы, разложение в степенной ряд.  График функции y = arcsin x
График функции y = arcsin x  График функции y = arccos x Арктангенс, арккотангенс – свойства, графики, формулы
График функции y = arccos x Арктангенс, арккотангенс – свойства, графики, формулы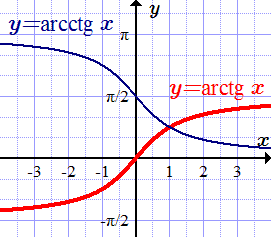 Даны все свойства арктангенса и арккотангенса, их графики, формулы, таблица арктангенсов и арккотангенсов. Выражения через комплексные числа, гиперболические функции. Производные, интегралы, разложения в степенные ряды.
Даны все свойства арктангенса и арккотангенса, их графики, формулы, таблица арктангенсов и арккотангенсов. Выражения через комплексные числа, гиперболические функции. Производные, интегралы, разложения в степенные ряды. 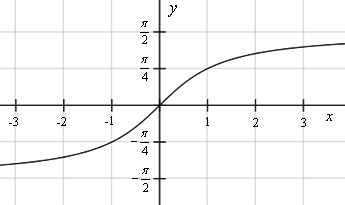 График функции y = arctg x.
График функции y = arctg x.  График функции y = arcctg x. Вывод формул обратных тригонометрических функций
График функции y = arcctg x. Вывод формул обратных тригонометрических функций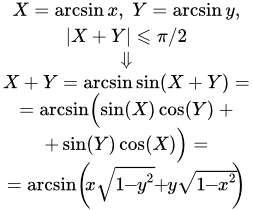 Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов. Выражение обратных тригонометрических функций комплексного переменного через логарифм
Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов. Выражение обратных тригонометрических функций комплексного переменного через логарифм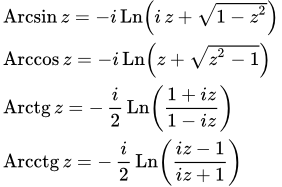 Даны формулы обратных тригонометрических функций, как функций комплексного переменного. Представлен вывод этих формул. Показано, что обратные тригонометрические функции выражаются через натуральные логарифмы.
Даны формулы обратных тригонометрических функций, как функций комплексного переменного. Представлен вывод этих формул. Показано, что обратные тригонометрические функции выражаются через натуральные логарифмы.  На рисунке изображена главная ветвь арксинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз.
На рисунке изображена главная ветвь арксинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз.  На рисунке изображена главная ветвь арккосинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз.
На рисунке изображена главная ветвь арккосинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз. 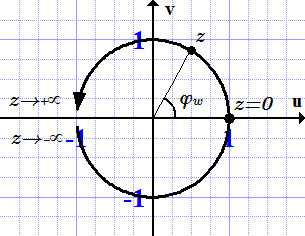 Комплексная функция ()(\displaystyle \small w(z)=\frac{1+iz}{1-iz} )() при действительных z.
Комплексная функция ()(\displaystyle \small w(z)=\frac{1+iz}{1-iz} )() при действительных z. 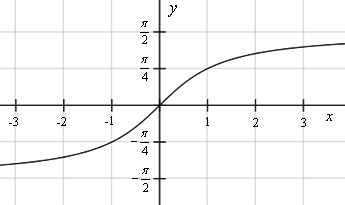 На рисунке изображена главная ветвь арктангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси.
На рисунке изображена главная ветвь арктангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси. 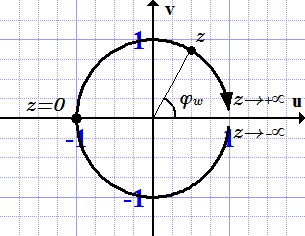 Комплексная функция ()(\displaystyle \small w(z)=\frac{iz-1}{iz+1} )() при действительных z.
Комплексная функция ()(\displaystyle \small w(z)=\frac{iz-1}{iz+1} )() при действительных z.  На рисунке изображена главная ветвь арккотангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси. Справочные данные по гиперболическим функциям – свойства, графики, формулы
На рисунке изображена главная ветвь арккотангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси. Справочные данные по гиперболическим функциям – свойства, графики, формулы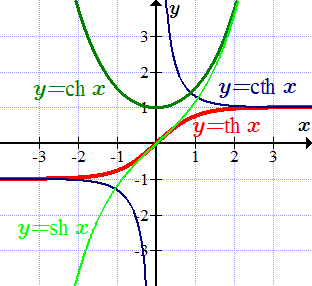 Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции.
Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции. 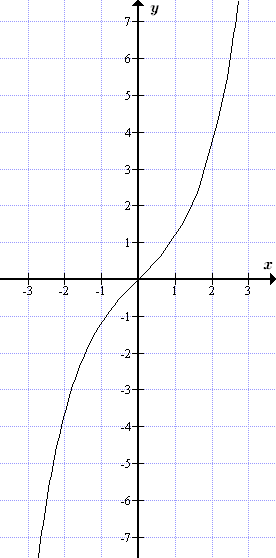 График гиперболического синуса y = sh x
График гиперболического синуса y = sh x 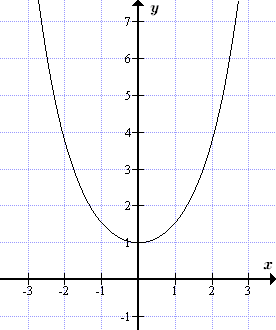 График гиперболического косинуса y = ch x
График гиперболического косинуса y = ch x 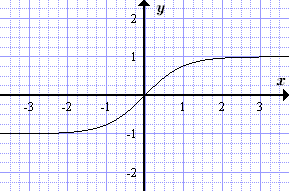 График гиперболического тангенса y = th x
График гиперболического тангенса y = th x 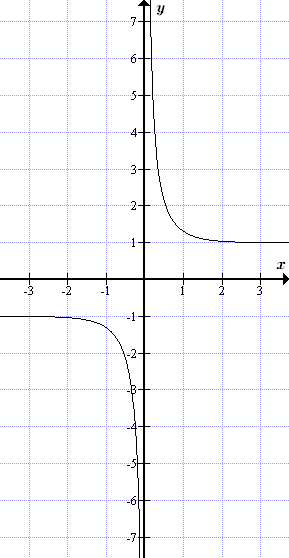 График гиперболического котангенса y = cth x Обратные гиперболические функции, их графики и формулы
График гиперболического котангенса y = cth x Обратные гиперболические функции, их графики и формулы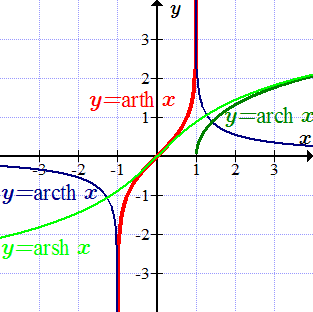 Даны определения обратных гиперболических функций и их графики. А также формулы, связывающие обратные гиперболические функции - формулы сумм и разностей. Выражения через тригонометрические функции. Производные, интегралы, разложения в ряды.
Даны определения обратных гиперболических функций и их графики. А также формулы, связывающие обратные гиперболические функции - формулы сумм и разностей. Выражения через тригонометрические функции. Производные, интегралы, разложения в ряды. 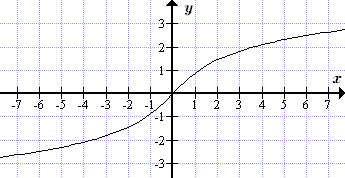 График обратного гиперболического синуса (ареасинуса) y = arsh x
График обратного гиперболического синуса (ареасинуса) y = arsh x 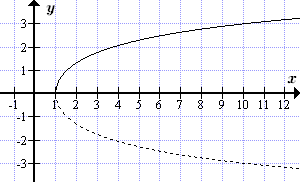 График обратного гиперболического косинуса (ареакосинуса) y = arch x , x ≥ 1
График обратного гиперболического косинуса (ареакосинуса) y = arch x , x ≥ 1
Пунктиром показана вторая ветвь ареакосинуса.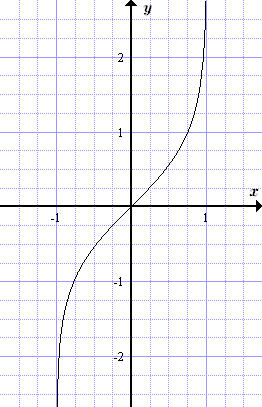 График обратного гиперболического тангенса (ареатангенса) y = arth x , |x| < 1
График обратного гиперболического тангенса (ареатангенса) y = arth x , |x| < 1 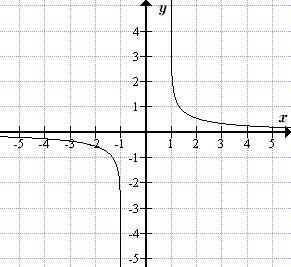 График обратного гиперболического котангенса (ареакотангенса) y = arcth x , |x| > 1 Корни квадратного уравнения
График обратного гиперболического котангенса (ареакотангенса) y = arcth x , |x| > 1 Корни квадратного уравнения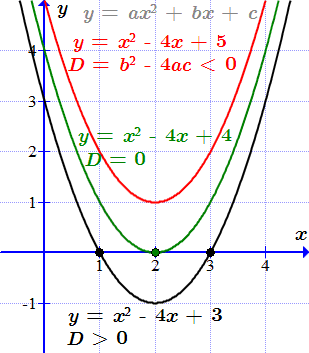 Формулы корней квадратного уравнения. Рассмотрены случаи действительных, кратных и комплексных корней. Разложение на множители квадратного трехчлена. Геометрическая интерпретация. Примеры определения корней и разложения на множители.
Формулы корней квадратного уравнения. Рассмотрены случаи действительных, кратных и комплексных корней. Разложение на множители квадратного трехчлена. Геометрическая интерпретация. Примеры определения корней и разложения на множители. 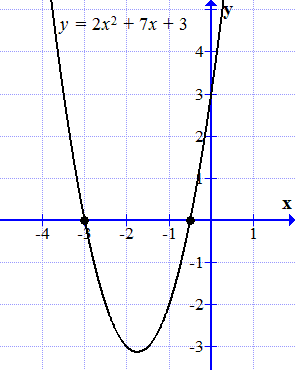 График функции y = 2x 2 + 7x + 3 пересекает ось абсцисс в двух точках.
График функции y = 2x 2 + 7x + 3 пересекает ось абсцисс в двух точках. 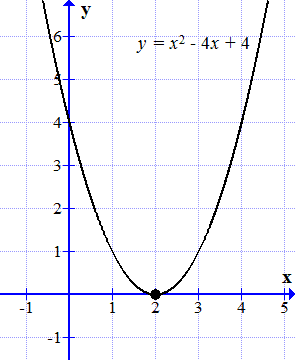 График функции y = x 2 – 4x + 4 касается оси абсцисс в одной точке.
График функции y = x 2 – 4x + 4 касается оси абсцисс в одной точке. 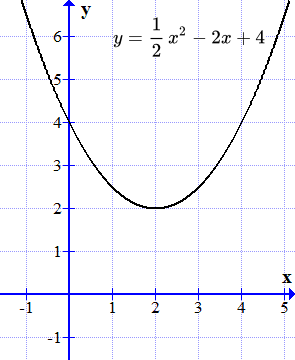 График функции не пересекает ось абсцисс. Действительных корней нет. Теорема Виета для квадратных и других уравнений
График функции не пересекает ось абсцисс. Действительных корней нет. Теорема Виета для квадратных и других уравнений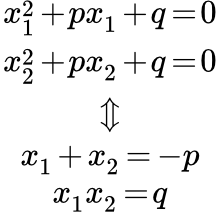 Формулировка и доказательство теоремы Виета для квадратных уравнений. Обратная теорема Виета. Теорема Виета для кубических уравнений и уравнений произвольного порядка. Решение квадратных уравнений онлайн (нахождение корней)
Формулировка и доказательство теоремы Виета для квадратных уравнений. Обратная теорема Виета. Теорема Виета для кубических уравнений и уравнений произвольного порядка. Решение квадратных уравнений онлайн (нахождение корней) Представлен онлайн калькулятор для нахождения корней квадратного уравнения. Пользователь вводит значения коэффициентов квадратного уравнения и получает его решение. Калькулятор рассчитывает не только корни, но и погрешности их определения, возникающие в результате округления чисел при выполнении вычислений. Значения коэффициентов можно вводить вместе с их погрешностями. Решение кубических уравнений
Представлен онлайн калькулятор для нахождения корней квадратного уравнения. Пользователь вводит значения коэффициентов квадратного уравнения и получает его решение. Калькулятор рассчитывает не только корни, но и погрешности их определения, возникающие в результате округления чисел при выполнении вычислений. Значения коэффициентов можно вводить вместе с их погрешностями. Решение кубических уравнений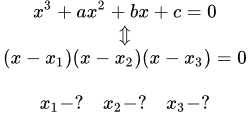 Изложено, как решать кубические уравнения. Рассмотрен случай, когда известен один корень. Методы поиска целых и рациональных корней. Применение формул Кардано и Виета для решения любого кубического уравнения. Формула Кардано для решения кубического уравнения
Изложено, как решать кубические уравнения. Рассмотрен случай, когда известен один корень. Методы поиска целых и рациональных корней. Применение формул Кардано и Виета для решения любого кубического уравнения. Формула Кардано для решения кубического уравнения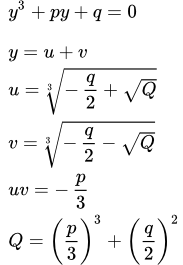 Здесь приводится вывод формулы Кардано для решения кубического уравнения. Тригонометрическая формула Виета для решения кубических уравнений
Здесь приводится вывод формулы Кардано для решения кубического уравнения. Тригонометрическая формула Виета для решения кубических уравнений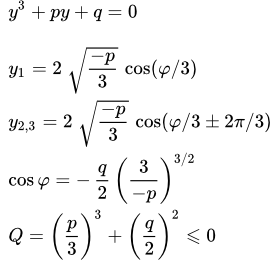 Здесь мы приводим вывод формулы Виета, используя формулу Кардано. Будет показано, что по формуле Виета удобно находить корни кубического уравнения в том случае, когда все три корня являются действительными числами. Примеры решений кубических уравнений
Здесь мы приводим вывод формулы Виета, используя формулу Кардано. Будет показано, что по формуле Виета удобно находить корни кубического уравнения в том случае, когда все три корня являются действительными числами. Примеры решений кубических уравнений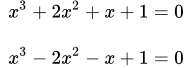 Приведены примеры решений кубических уравнений по формулам Кардано и Виета. Онлайн калькулятор корней кубических уравнений
Приведены примеры решений кубических уравнений по формулам Кардано и Виета. Онлайн калькулятор корней кубических уравнений Онлайн калькулятор для нахождения корней кубического уравнения. Вы вводите коэффициенты кубического уравнения и получаете его решение. Основные виды неравенств и их свойства
Онлайн калькулятор для нахождения корней кубического уравнения. Вы вводите коэффициенты кубического уравнения и получаете его решение. Основные виды неравенств и их свойства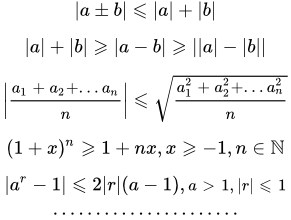 Представлены основные виды неравенств, включая неравенства Бернулли, Коши - Буняковского, Минковского, Чебышева. Рассмотрены свойства неравенств и действия над ними. Даны основные методы решения неравенств.
Представлены основные виды неравенств, включая неравенства Бернулли, Коши - Буняковского, Минковского, Чебышева. Рассмотрены свойства неравенств и действия над ними. Даны основные методы решения неравенств.
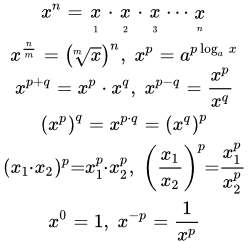 Приведены основные свойства степенной функции, включая формулы и свойства корней. Представлены производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел степенной функции.
Приведены основные свойства степенной функции, включая формулы и свойства корней. Представлены производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел степенной функции.  Графики степенной функции y = x p при различных значениях показателя p. Степенная функция, ее свойства и графики
Графики степенной функции y = x p при различных значениях показателя p. Степенная функция, ее свойства и графики Представлены свойства и графики степенных функций при различных значениях показателя степени. Основные формулы, области определения и множества значений, четность, монотонность, возрастание и убывание, экстремумы, выпуклость, перегибы, точки пересечения с осями координат, пределы, частные значения.
Представлены свойства и графики степенных функций при различных значениях показателя степени. Основные формулы, области определения и множества значений, четность, монотонность, возрастание и убывание, экстремумы, выпуклость, перегибы, точки пересечения с осями координат, пределы, частные значения.  Графики степенной функции y = xn с натуральным нечетным показателем n = 1, 3, 5, ....
Графики степенной функции y = xn с натуральным нечетным показателем n = 1, 3, 5, ....  Графики степенной функции y = xn с натуральным четным показателем n = 2, 4, 6, ....
Графики степенной функции y = xn с натуральным четным показателем n = 2, 4, 6, ....  Графики степенной функции y = xn с целым отрицательным показателем n = -1, -2, -3, ....
Графики степенной функции y = xn с целым отрицательным показателем n = -1, -2, -3, ....  Графикии степенных функций y = xp = xn/m с рациональным отрицательным показателем p = n/m, где m = 3, 5, 7, ... - нечетное.
Графикии степенных функций y = xp = xn/m с рациональным отрицательным показателем p = n/m, где m = 3, 5, 7, ... - нечетное.  Графики степенной функции y = xp = xn/m с рациональным показателем p = n/m, где m = 3, 5, 7, ... - нечетное, 0 < p < 1.
Графики степенной функции y = xp = xn/m с рациональным показателем p = n/m, где m = 3, 5, 7, ... - нечетное, 0 < p < 1.  Графики степенной функции y = xp = xn/m с рациональным показателем p = n/m, где m = 3, 5, 7, ... - нечетное, p > 1. Показательная функция – свойства, графики, формулы
Графики степенной функции y = xp = xn/m с рациональным показателем p = n/m, где m = 3, 5, 7, ... - нечетное, p > 1. Показательная функция – свойства, графики, формулы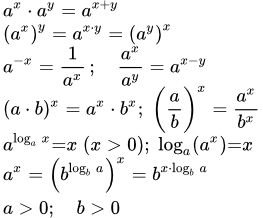 Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.  Графики показательной функции y = ax при различных значениях основания a. Логарифм - свойства, формулы, график
Графики показательной функции y = ax при различных значениях основания a. Логарифм - свойства, формулы, график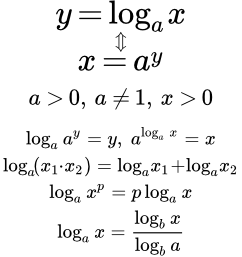 Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.  Графики логарифма y = loga x при различных значениях основания a. Экспонента, е в степени х
Графики логарифма y = loga x при различных значениях основания a. Экспонента, е в степени х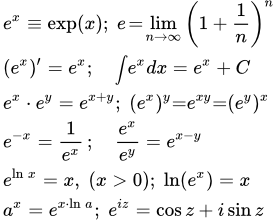 Приведены график и основные свойства экспоненты (е в степени х): область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд, действия с комплексными числами.
Приведены график и основные свойства экспоненты (е в степени х): область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд, действия с комплексными числами.  График экспоненты, y = ex. Натуральный логарифм, функция ln x
График экспоненты, y = ex. Натуральный логарифм, функция ln x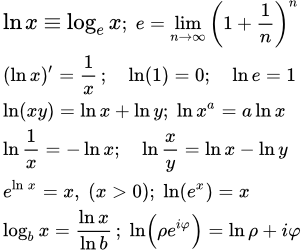 Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.  График функции y = ln x. Синус (sin x) и косинус (cos x) – свойства, графики, формулы
График функции y = ln x. Синус (sin x) и косинус (cos x) – свойства, графики, формулы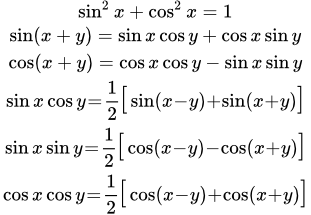 Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.  Геометрическое определение синуса и косинуса
Геометрическое определение синуса и косинуса  Графики функций y=sin(x) и y=cos(x).
Графики функций y=sin(x) и y=cos(x). 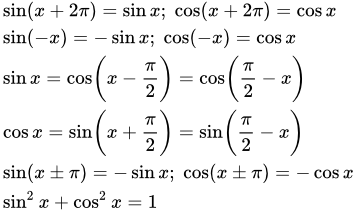 Периодичность, четность и основные формулы синуса и косинуса
Периодичность, четность и основные формулы синуса и косинуса 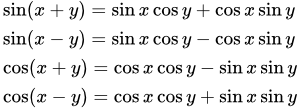 Формулы синуса и косинуса от суммы и разности аргументов
Формулы синуса и косинуса от суммы и разности аргументов 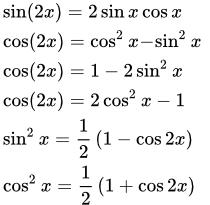 Синус и косинуса двойного угла.
Синус и косинуса двойного угла. 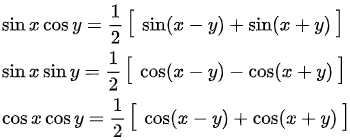 Формулы произведения синусов и косинусов
Формулы произведения синусов и косинусов 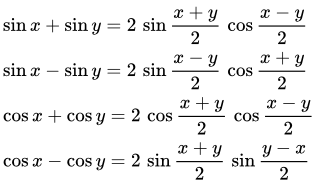 Формулы суммы и разности синуса и косинуса
Формулы суммы и разности синуса и косинуса 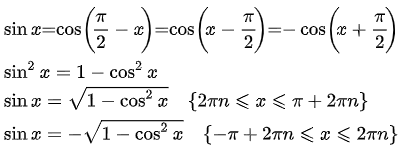 Выражение синуса через косинус
Выражение синуса через косинус 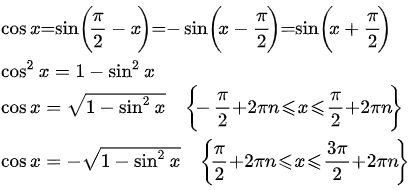 Выражение косинуса через синус
Выражение косинуса через синус 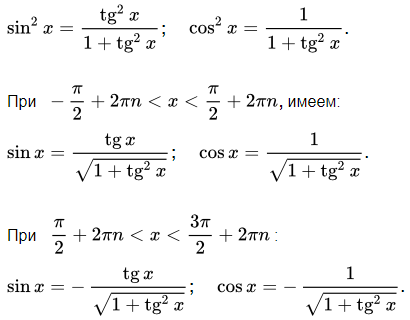 Выражение синуса и косинуса через тангенс
Выражение синуса и косинуса через тангенс 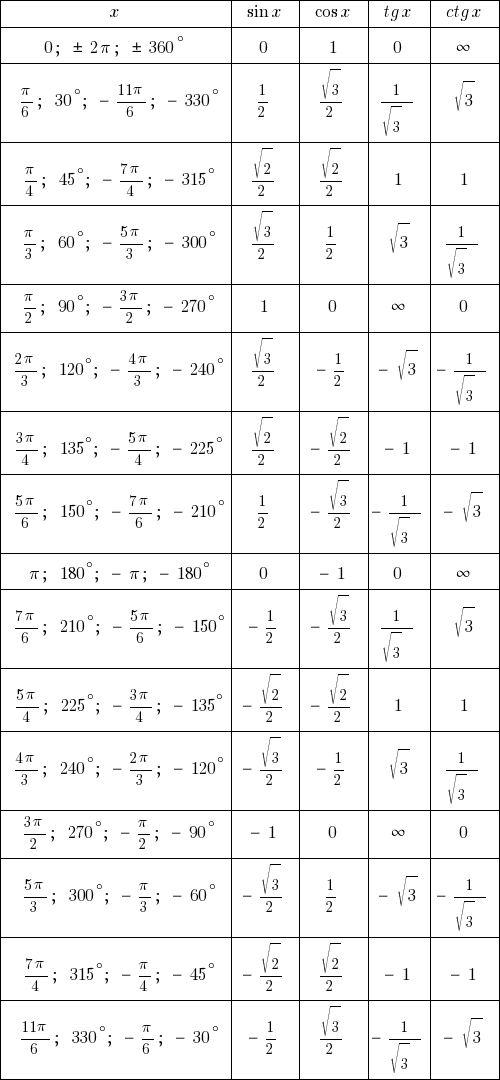 Таблица синусов и косинусов Тангенс (tg x) и котангенс (ctg x) – свойства, графики, формулы
Таблица синусов и косинусов Тангенс (tg x) и котангенс (ctg x) – свойства, графики, формулы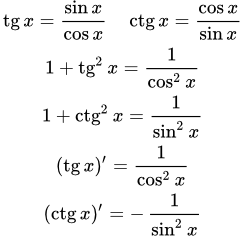 Справочные данные по тангенсу (tg x) и котангенсу (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица тангенсов и котангенсов, производные, интегралы, разложения в ряды. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Справочные данные по тангенсу (tg x) и котангенсу (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица тангенсов и котангенсов, производные, интегралы, разложения в ряды. Выражения через комплексные переменные. Связь с гиперболическими функциями.  Геометрическое определение тангенса и котангенса
Геометрическое определение тангенса и котангенса  Графики функций y=tg(x) и y=ctg(x).
Графики функций y=tg(x) и y=ctg(x). 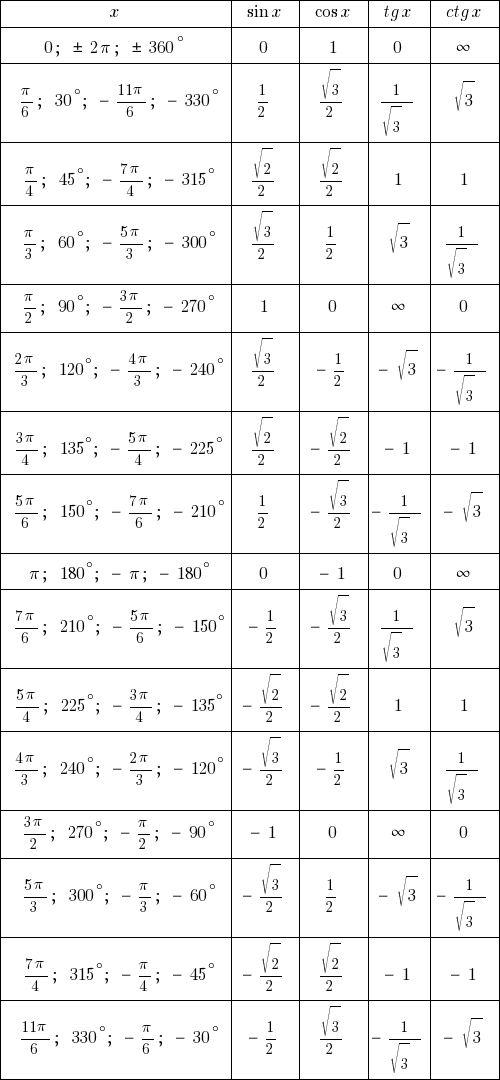 Таблица тангенсов и котангенсов Обратные тригонометрические функции, их графики и формулы
Таблица тангенсов и котангенсов Обратные тригонометрические функции, их графики и формулы Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.
Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.  y = arcsin x
y = arcsin x  y = arccos x
y = arccos x 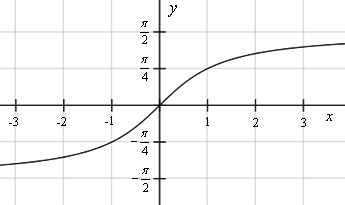 y = arctg x
y = arctg x  y = arcctg x Арксинус, арккосинус - свойства, графики, формулы
y = arcctg x Арксинус, арккосинус - свойства, графики, формулы Даны свойства арксинуса и арккосинуса, их графики, формулы, таблица арксинусов и арккосинусов. Выражения через комплексные числа, гиперболические функции. Производные, интегралы, разложение в степенной ряд.
Даны свойства арксинуса и арккосинуса, их графики, формулы, таблица арксинусов и арккосинусов. Выражения через комплексные числа, гиперболические функции. Производные, интегралы, разложение в степенной ряд.  График функции y = arcsin x
График функции y = arcsin x  График функции y = arccos x Арктангенс, арккотангенс – свойства, графики, формулы
График функции y = arccos x Арктангенс, арккотангенс – свойства, графики, формулы Даны все свойства арктангенса и арккотангенса, их графики, формулы, таблица арктангенсов и арккотангенсов. Выражения через комплексные числа, гиперболические функции. Производные, интегралы, разложения в степенные ряды.
Даны все свойства арктангенса и арккотангенса, их графики, формулы, таблица арктангенсов и арккотангенсов. Выражения через комплексные числа, гиперболические функции. Производные, интегралы, разложения в степенные ряды. 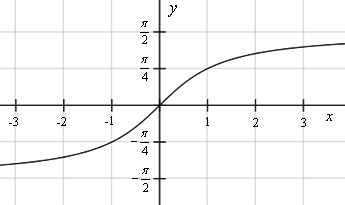 График функции y = arctg x.
График функции y = arctg x.  График функции y = arcctg x. Вывод формул обратных тригонометрических функций
График функции y = arcctg x. Вывод формул обратных тригонометрических функций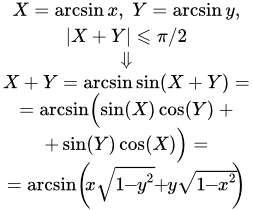 Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов. Выражение обратных тригонометрических функций комплексного переменного через логарифм
Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов. Выражение обратных тригонометрических функций комплексного переменного через логарифм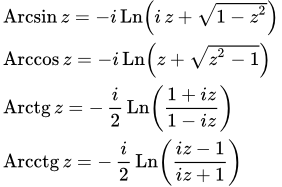 Даны формулы обратных тригонометрических функций, как функций комплексного переменного. Представлен вывод этих формул. Показано, что обратные тригонометрические функции выражаются через натуральные логарифмы.
Даны формулы обратных тригонометрических функций, как функций комплексного переменного. Представлен вывод этих формул. Показано, что обратные тригонометрические функции выражаются через натуральные логарифмы.  На рисунке изображена главная ветвь арксинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз.
На рисунке изображена главная ветвь арксинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз.  На рисунке изображена главная ветвь арккосинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз.
На рисунке изображена главная ветвь арккосинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз. 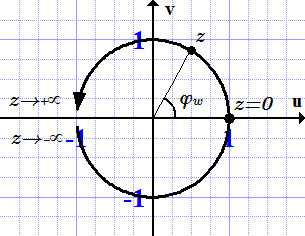 Комплексная функция ()(\displaystyle \small w(z)=\frac{1+iz}{1-iz} )() при действительных z.
Комплексная функция ()(\displaystyle \small w(z)=\frac{1+iz}{1-iz} )() при действительных z. 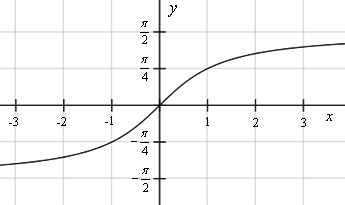 На рисунке изображена главная ветвь арктангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси.
На рисунке изображена главная ветвь арктангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси.  Комплексная функция ()(\displaystyle \small w(z)=\frac{iz-1}{iz+1} )() при действительных z.
Комплексная функция ()(\displaystyle \small w(z)=\frac{iz-1}{iz+1} )() при действительных z.  На рисунке изображена главная ветвь арккотангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси. Справочные данные по гиперболическим функциям – свойства, графики, формулы
На рисунке изображена главная ветвь арккотангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси. Справочные данные по гиперболическим функциям – свойства, графики, формулы Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции.
Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции.  График гиперболического синуса y = sh x
График гиперболического синуса y = sh x  График гиперболического косинуса y = ch x
График гиперболического косинуса y = ch x  График гиперболического тангенса y = th x
График гиперболического тангенса y = th x  График гиперболического котангенса y = cth x Обратные гиперболические функции, их графики и формулы
График гиперболического котангенса y = cth x Обратные гиперболические функции, их графики и формулы Даны определения обратных гиперболических функций и их графики. А также формулы, связывающие обратные гиперболические функции - формулы сумм и разностей. Выражения через тригонометрические функции. Производные, интегралы, разложения в ряды.
Даны определения обратных гиперболических функций и их графики. А также формулы, связывающие обратные гиперболические функции - формулы сумм и разностей. Выражения через тригонометрические функции. Производные, интегралы, разложения в ряды.  График обратного гиперболического синуса (ареасинуса) y = arsh x
График обратного гиперболического синуса (ареасинуса) y = arsh x  График обратного гиперболического косинуса (ареакосинуса) y = arch x , x ≥ 1
График обратного гиперболического косинуса (ареакосинуса) y = arch x , x ≥ 1 Пунктиром показана вторая ветвь ареакосинуса.
 График обратного гиперболического тангенса (ареатангенса) y = arth x , |x| < 1
График обратного гиперболического тангенса (ареатангенса) y = arth x , |x| < 1  График обратного гиперболического котангенса (ареакотангенса) y = arcth x , |x| > 1 Корни квадратного уравнения
График обратного гиперболического котангенса (ареакотангенса) y = arcth x , |x| > 1 Корни квадратного уравнения Формулы корней квадратного уравнения. Рассмотрены случаи действительных, кратных и комплексных корней. Разложение на множители квадратного трехчлена. Геометрическая интерпретация. Примеры определения корней и разложения на множители.
Формулы корней квадратного уравнения. Рассмотрены случаи действительных, кратных и комплексных корней. Разложение на множители квадратного трехчлена. Геометрическая интерпретация. Примеры определения корней и разложения на множители. 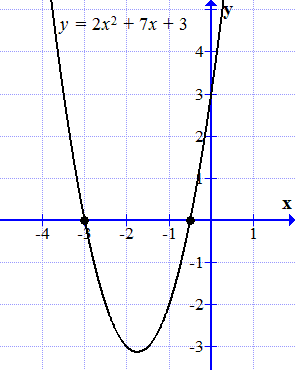 График функции y = 2x 2 + 7x + 3 пересекает ось абсцисс в двух точках.
График функции y = 2x 2 + 7x + 3 пересекает ось абсцисс в двух точках.  График функции y = x 2 – 4x + 4 касается оси абсцисс в одной точке.
График функции y = x 2 – 4x + 4 касается оси абсцисс в одной точке.  График функции не пересекает ось абсцисс. Действительных корней нет. Теорема Виета для квадратных и других уравнений
График функции не пересекает ось абсцисс. Действительных корней нет. Теорема Виета для квадратных и других уравнений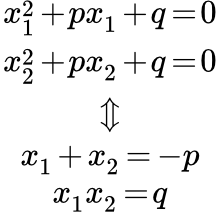 Формулировка и доказательство теоремы Виета для квадратных уравнений. Обратная теорема Виета. Теорема Виета для кубических уравнений и уравнений произвольного порядка. Решение квадратных уравнений онлайн (нахождение корней)
Формулировка и доказательство теоремы Виета для квадратных уравнений. Обратная теорема Виета. Теорема Виета для кубических уравнений и уравнений произвольного порядка. Решение квадратных уравнений онлайн (нахождение корней) Представлен онлайн калькулятор для нахождения корней квадратного уравнения. Пользователь вводит значения коэффициентов квадратного уравнения и получает его решение. Калькулятор рассчитывает не только корни, но и погрешности их определения, возникающие в результате округления чисел при выполнении вычислений. Значения коэффициентов можно вводить вместе с их погрешностями. Решение кубических уравнений
Представлен онлайн калькулятор для нахождения корней квадратного уравнения. Пользователь вводит значения коэффициентов квадратного уравнения и получает его решение. Калькулятор рассчитывает не только корни, но и погрешности их определения, возникающие в результате округления чисел при выполнении вычислений. Значения коэффициентов можно вводить вместе с их погрешностями. Решение кубических уравнений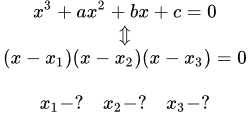 Изложено, как решать кубические уравнения. Рассмотрен случай, когда известен один корень. Методы поиска целых и рациональных корней. Применение формул Кардано и Виета для решения любого кубического уравнения. Формула Кардано для решения кубического уравнения
Изложено, как решать кубические уравнения. Рассмотрен случай, когда известен один корень. Методы поиска целых и рациональных корней. Применение формул Кардано и Виета для решения любого кубического уравнения. Формула Кардано для решения кубического уравнения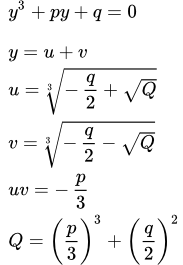 Здесь приводится вывод формулы Кардано для решения кубического уравнения. Тригонометрическая формула Виета для решения кубических уравнений
Здесь приводится вывод формулы Кардано для решения кубического уравнения. Тригонометрическая формула Виета для решения кубических уравнений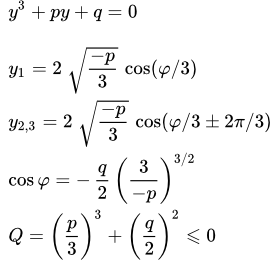 Здесь мы приводим вывод формулы Виета, используя формулу Кардано. Будет показано, что по формуле Виета удобно находить корни кубического уравнения в том случае, когда все три корня являются действительными числами. Примеры решений кубических уравнений
Здесь мы приводим вывод формулы Виета, используя формулу Кардано. Будет показано, что по формуле Виета удобно находить корни кубического уравнения в том случае, когда все три корня являются действительными числами. Примеры решений кубических уравнений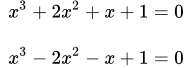 Приведены примеры решений кубических уравнений по формулам Кардано и Виета. Онлайн калькулятор корней кубических уравнений
Приведены примеры решений кубических уравнений по формулам Кардано и Виета. Онлайн калькулятор корней кубических уравнений Онлайн калькулятор для нахождения корней кубического уравнения. Вы вводите коэффициенты кубического уравнения и получаете его решение. Основные виды неравенств и их свойства
Онлайн калькулятор для нахождения корней кубического уравнения. Вы вводите коэффициенты кубического уравнения и получаете его решение. Основные виды неравенств и их свойства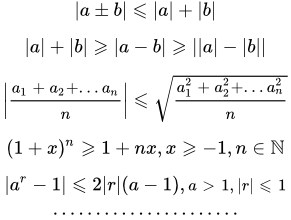 Представлены основные виды неравенств, включая неравенства Бернулли, Коши - Буняковского, Минковского, Чебышева. Рассмотрены свойства неравенств и действия над ними. Даны основные методы решения неравенств.
Представлены основные виды неравенств, включая неравенства Бернулли, Коши - Буняковского, Минковского, Чебышева. Рассмотрены свойства неравенств и действия над ними. Даны основные методы решения неравенств. 