Теоремы о существовании и непрерывности обратной функции

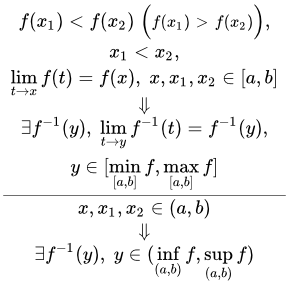
Теорема о существовании и непрерывности обратной функции на отрезке

Пусть функция непрерывна
и строго возрастает (строго убывает) на отрезке .
Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (строго убывает).
Для возрастающей функции .
Для убывающей: .

Доказательство

Пусть обозначает область определения функции – отрезок .

1. Множество значений функции f

1. Покажем, что множеством значений функции является отрезок :
,
где .

Действительно, поскольку функция непрерывна на отрезке , то по теореме Вейерштрасса она достигает на нем минимума и максимума . Тогда по теореме Больцано – Коши функция принимает все значения из отрезка . То есть для любого существует , для которого . Поскольку и есть минимум и максимум, то функция принимает на отрезке только значения из множества .

2. Существование и монотонность обратной функции

2. Поскольку функция строго монотонна, то согласно теореме о существовании и монотонности обратной функции, существует обратная функция , которая также строго монотонна (возрастает, если возрастает ; и убывает, если убывает ). Областью определения обратной функции является множество , а множеством значений – множество .

3. Доказательство непрерывности

3. Теперь докажем, что обратная функция непрерывна.

3.1. Функция строго возрастает

3.1. Пусть строго возрастает. При этом обратная функция также строго возрастает; .

3.1.1. Внутренняя точка отрезка

3.1.1. Пусть есть произвольная внутренняя точка отрезка : . Докажем, что обратная функция непрерывна в этой точке.

Поскольку обратная функция строго монотонна, то есть внутренняя точка отрезка :
.

Согласно определению непрерывности, нам нужно доказать, что для любого имеется такая функция , при которой
(3.1)   для всех .

При доказательстве мы используем следующие обозначения:


.

Рассмотрим и преобразуем неравенство:
;
;
;
(3.2)   .

Возьмем произвольное положительное число ε. Положим
.
Если числа и/или выходят за границы отрезка , то положим , и/или . То есть возьмем
.
Используя (3.2), для (3.1) имеем:
(3.3)   .

Как мы только что выяснили, существует обратная функция , и она строго возрастает. Тогда если значения переменной y принадлежат интервалу , то значения переменной x принадлежат интервалу . Возьмем . Тогда
.
То есть все значения переменной y, принадлежащие интервалу , принадлежат интервалу . Но можно записать как . То есть для всех значений y из интервала , значения обратной функции принадлежат интервалу . А учитывая (3.3), они также принадлежат интервалу , что можно записать как , или .

То есть мы нашли такую функцию

,
так что для всех значений переменной y из интервала , значения переменной x принадлежат интервалу , или . То есть мы получили (3.1). Поскольку мы взяли произвольное , то это означает, что обратная функция непрерывна в точке .

Поскольку является произвольной внутренней точкой отрезка , то это означает, что обратная функция непрерывна во всех точках .

3.1.2. Точка a

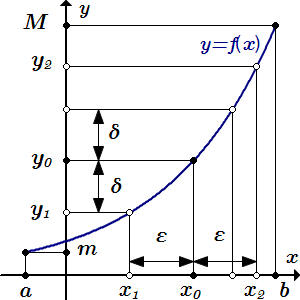
Теперь докажем, что обратная функция непрерывна в точке m – на нижнем конце отрезка : . Согласно определению, нам нужно показать, что правый предел при равен значению обратной функции в точке m:
.

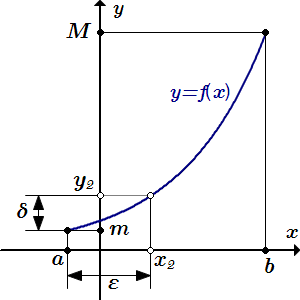
Согласно определению одностороннего предела, нам нужно показать, что для любого существует , так что для всех , значения обратной функции лежат в правой ε-окрестности точки :
.
Здесь мы учли, что в определении непрерывности вместо проколотой окрестности , как в определении предела, можно использовать просто окрестность . Хотя это и необязательно.

Возьмем произвольное . Введем обозначения:
.
Тогда в силу строгого возрастания обратной функции, при , ее значения лежат в полуинтервале , который можно выразить через переменную x:
.
То есть мы должны взять . Тогда для всех y из правой δ-окрестности точки m: , значения обратной функции принадлежат правой ε-окрестности точки :
.
Это означает, что . То есть обратная функция непрерывна в точке m, на конце отрезка .

3.1.3. Точка b

Аналогичным образом докажем, что обратная функция непрерывна в точке M – на верхнем конце отрезка : . Нам нужно показать, что левый предел при равен значению обратной функции в точке M:
.

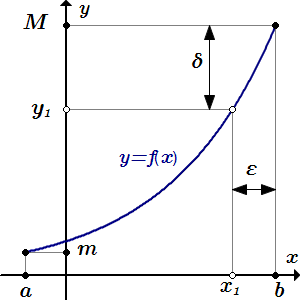
Покажем, что для любого существует , так что для всех , значения обратной функции лежат в левой ε-окрестности точки :
.

Возьмем произвольное . Введем обозначения:
.
Тогда в силу строгого возрастания обратной функции, при , ее значения лежат в полуинтервале , который можно выразить через переменную x:
.
То есть мы должны взять . Тогда для всех y из левой δ-окрестности точки M: , значения обратной функции принадлежат левой ε-окрестности точки :
.
Это означает, что . То есть обратная функция непрерывна в точке M, на правом конце отрезка .

3.1.4. Более простое доказательство

Заметим, что мы можем упростить доказательство непрерывности обратной функции, заменив пункт 3.1.1 более простыми рассуждениями. Для этого сначала нужно выполнить доказательства пунктов 3.1.2 и 3.1.3, в которых мы доказываем, что обратная функция непрерывна на концах отрезка, то есть имеет односторонние пределы:
.
Далее нужно взять произвольную точку внутри отрезка , и разбить его на два отрезка: и . Поскольку обратная функция непрерывна на концах отрезков, то
.
Тогда, согласно свойству о равенстве односторонних пределов, обратная функция имеет в точке предел
.
Поскольку предел при равен значению обратной функции в , то она непрерывна в .

3.2. Функция строго убывает

3.2. Теперь рассмотрим случай, когда строго убывает. Она имеет минимальное и максимальное значения:
.
Как показано в пунктах 1 и 2, она имеет обратную функцию , которая определена на отрезке , и строго убывает.

Для доказательства непрерывности, рассмотрим функцию . Функция строго возрастает, она определена и непрерывна при . Ее минимальное и максимальное значения:

.
Согласно доказанному в пункте 3.1, ее обратная функция непрерывна на отрезке .

Выразим через , пользуясь свойствами обратных функций и учитывая, что :
.
Итак, мы нашли, что
(3.2.1)   .

Представим функцию как сложную:
,
где .
Функция непрерывна для всех y, в том числе и на отрезке , который она отображает в отрезок . Функция непрерывна на этом отрезке. Тогда по теореме о непрерывности сложной функции, функция непрерывна при .

Теорема доказана.

Теорема о существовании и непрерывности обратной функции на интервале

Пусть функция непрерывна
и строго возрастает (строго убывает) на открытом конечном или бесконечном интервале .
Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (строго убывает).
Для возрастающей функции .
Для убывающей: .

Доказательство

1. Существование обратной функции

1. Пусть обозначает область определения функции – открытый интервал . Пусть – множество ее значений при . Согласно теореме о существовании и монотонности обратной функции, существует обратная функция , которая имеет область определения , множество значений и является строго монотонной (возрастает если возрастает и убывает если убывает ). Нам осталось доказать следующее.
2) Множеством является открытый интервал ,
где для возрастающей функции: ;
для убывающей функции: .
3) Обратная функция непрерывна на интервале .

2. Множество значений обратной функции

2. Покажем, что множеством значений функции является открытый интервал :
.

Как и всякое непустое множество, элементы которого имеют операцию сравнения, множество значений функции имеет нижнюю и верхнюю грани:
.
Здесь и могут быть конечными числами или символами и .

Согласно теореме о пределе монотонной функции,
для возрастающей функции ;
для убывающей функции .

2.1. Покажем, что точки и не принадлежат множеству значений функции. То есть множество значений не может быть отрезком .

Если или является бесконечно удаленной точкой: или , то такая точка не является элементом множества. Поэтому она не может принадлежать множеству значений.

Пусть (или ) является конечным числом. Допустим противное. Пусть точка (или ) принадлежит множеству значений функции . То есть существует такое , для которого (или ). Возьмем точки и , удовлетворяющие неравенствам:
.
Поскольку функция строго монотонна, то
, если f возрастает;
, если f убывает.
То есть мы нашли точку, значение функции в которой меньше (больше ). Но это противоречит определению нижней (верхней) грани, согласно которому
для всех .
Поэтому точки и не могут принадлежать множеству значений функции .

2.2. Покажем, что обратная функция определена в произвольной точке . То есть нам нужно показать, что существует такое число , так что .

Возьмем произвольное число , принадлежащее интервалу : .
Поскольку , или , то в любой проколотой ε-окрестности точи m существует такое значение , что принадлежит этой окрестности. Возьмем . Тогда существует такое , так что .
Аналогичным образом, поскольку , если строго возрастает, или , если строго убывает, то существует такое значение , так что .

Итак, мы выяснили, что существует такой отрезок (или ), на котором функция непрерывна, и
.
Тогда по второй теореме Больцано – Коши о промежуточном значении, существует такое число , так что .

3. Непрерывность обратной функции

3. Теперь покажем, что обратная функция непрерывна в произвольной точке интервала :  .

В предыдущем пункте 2.2 мы показали, что существует такое , так что . Там же мы показали, что существуют такие и , так что
.
В силу строгой монотонности функции отсюда следует, что
, если f строго возрастает, или
, если f строго убывает.

Таким образом, функция определена, непрерывна и строго монотонна на отрезке (или ). Тогда согласно предыдущей теореме ⇑, обратная функция непрерывна на отрезке , в том числе и в точке .

Теорема доказана.

Теорема о существовании и непрерывности обратной функции на полуинтервале

Пусть функция непрерывна и строго монотонна на полуинтервале X.
Тогда на полуинтервале Y определена, строго монотонна и непрерывна обратная функция .
Если строго возрастает, то также строго возрастает. При этом:
если , то ;
если , то .
Если строго убывает, то также строго убывает. При этом:
если , то ;
если , то .
Здесь . Открытый конец интервала может быть конечным числом или бесконечно удаленной точкой.

Доказательство

Пусть функция определена, непрерывна и строго возрастает на полуинтервале .

Произвольным образом выберем две точки и такие, что
(p.1)   .
Тогда функция определена, непрерывна и строго возрастает на отрезке . Поэтому по теорема о существовании и непрерывности обратной функции на отрезке, на отрезке определена и непрерывна обратная функция , которая строго возрастает.

Также функция определена, непрерывна и строго возрастает на интервале . Поэтому по теорема о существовании и непрерывности обратной функции на интервале, на интервале определена и непрерывна обратная функция , которая строго возрастает.

Найдем объединение интервалов и . Поскольку функция строго монотонна, то в силу (p.1) имеем:
.
Тогда отрезок и интервал перекрываются. Их объединение: . Это означает, что при определена и непрерывна обратная функция , которая строго возрастает.

Для строго возрастающей функции и теорема доказана.

Аналогичным способом можно рассмотреть случай и случаи строго убывающей функции .