Свойства непрерывных в точке функций
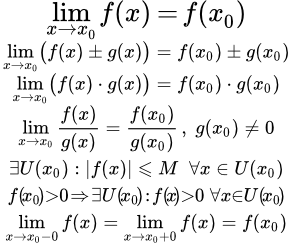
Свойства и теоремы
Теорема об ограниченности непрерывной функции
Пусть функция f(x) непрерывна в точке x0. Тогда существует такая окрестность U(x0), на которой функция ограничена.
Доказательство ⇓
Теорема о сохранении знака непрерывной функции
Пусть функция f(x) непрерывна в точке x0. И пусть она имеет положительное (отрицательное) значение в этой точке:
f(x0) > 0 ( f(x0) < 0 ).
Тогда существует такая окрестность U(x0) точки x0, на которой функция имеет положительное (отрицательное) значение:
f(x) > 0 ( f(x) < 0 ) при x ∈ U(x0).
Доказательство ⇓
Арифметические свойства непрерывных функций
Пусть функции f(x) и g(x) непрерывны в точке x0.
Тогда сумма f(x) + g(x), разность f(x) – g(x) и произведение f(x) · g(x) функций непрерывны в точке x0.
Если g(x0) ≠ 0, то и частное функций f(x) / g(x) непрерывно в точке x0.
Доказательство ⇓
Свойство непрерывности слева и справа
Функция f непрерывна в точке x0 тогда и только тогда, когда она непрерывна в x0 слева и справа.
Доказательство ⇓
Доказательства свойств и теорем
Теорема об ограниченности непрерывной функции
Все свойства ⇑ Пусть функция f(x) непрерывна в точке x0. Тогда существует такая окрестность U(x0), на которой функция ограничена.
Доказательство
Воспользуемся определением непрерывности функции в точке по Коши. Согласно этому определению имеется такая функция , что для любого ,
при .
Положим . Тогда при имеем:
.
Раскроем знак модуля и преобразуем неравенства.
;
.
Пусть M есть наибольшее из чисел: . Тогда
, или
.
Итак, мы нашли окрестность , на которой функция ограничена числом :
.
Теорема доказана.
Теорема о сохранении знака непрерывной функции
Все свойства ⇑ Пусть функция f(x) непрерывна в точке x0. И пусть она имеет положительное (отрицательное) значение в этой точке:
f(x0) > 0 ( f(x0) < 0 ).
Тогда существует такая окрестность U(x0) точки x0, на которой функция имеет положительное (отрицательное) значение:
f(x) > 0 ( f(x) < 0 ) при x ∈ U(x0).
Доказательство
Воспользуемся определением непрерывности функции в точке по Коши. Согласно этому определению имеется такая функция , что для любого ,
при .
Положим . Тогда при имеем:
(1) .
Пусть . Раскроем в (1) знак модуля и преобразуем неравенства:
;
;
.
Итак, мы нашли окрестность , на которой функция ограничена снизу положительным числом:
.
Поэтому на этой окрестности функция имеет положительное значение:
.
Для случая теорема доказана.
Теперь рассмотрим случай . Также раскрываем в (1) знак модуля и преобразуем неравенства:
;
;
;
.
Тем самым мы нашли окрестность , на которой функция ограничена сверху отрицательным числом:
.
Поэтому на этой окрестности .
Теорема доказана.
Арифметические свойства непрерывных функций
Все свойства ⇑ Пусть функции f(x) и g(x) непрерывны в точке x0.
Тогда сумма f(x) + g(x), разность f(x) – g(x) и произведение f(x) · g(x) функций непрерывны в точке x0.
Если g(x0) ≠ 0, то и частное функций f(x) / g(x) непрерывно в точке x0.
Доказательство
Воспользуемся определением непрерывности функции в точке. Согласно этому определению, Функция называется непрерывной в точке , если она определена на некоторой окрестности этой точки, и если предел при стремящемся к существует и равен значению функции в :
.
Поскольку функции и непрерывны в точке , то они определены на некоторых окрестностях и , соответственно, этой точки. Пусть окрестность является пересечением окрестностей и . Тогда обе функции и определены на окрестности .
Поскольку функции и определены на окрестности , то они определены и на проколотой окрестности точки , которая получается из исключением точки .
Итак, функции и определены на некоторой проколотой окрестности конечной точки , и существуют их пределы:
и .
Тогда, согласно арифметическим свойствам пределов функции, существуют пределы суммы, разности и произведения функций:
;
;
.
Если , то существует предел частного:
.
Свойства доказаны.
Свойство непрерывности слева и справа
Все свойства ⇑ Функция f непрерывна в точке x0 тогда и только тогда, когда она непрерывна в x0 слева и справа.
Доказательство
1) Пусть функция непрерывна в точке . Докажем, что она непрерывна в справа и слева.
Воспользуемся определением непрерывности функции в точке по Коши. Согласно этому определению, имеется такая функция , так что для любого ,
(2) при .
Поскольку неравенство выполняется для любых значений , принадлежащих окрестности , то наложим дополнительное ограничение: . Тогда
для любого , имеется , так что
при .
Это означает, что . То есть функция непрерывна в справа.
Теперь, в (2), наложим ограничение . Тогда
для любого , имеется , так что
при .
Это означает, что . То есть функция непрерывна в слева.
Первая часть свойства доказана.
2) Теперь пусть функция непрерывна в точке x0 слева и справа.
Поскольку функция непрерывна слева, то имеется такая функция , так что для любого ,
при .
Поскольку функция непрерывна в точке справа, то имеется такая функция , так что для любого ,
при .
Пусть . Тогда . Если принадлежит окрестности , то также принадлежит окрестности . Поэтому
при .
Аналогично, если , то . Поэтому
при .
Итак, мы нашли такую функцию , при которой для любого ,
при .
Это означает, что . То есть функция является непрерывной в точке .
Свойство доказано.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
