Определение непрерывности функции в точке

Приводится определение непрерывности функции в точке. Рассмотрены эквивалентные определения по Гейне, по Коши и в терминах приращений. Определение односторонней непрерывности на концах отрезка. Формулировка отсутствия непрерывности. Разобраны примеры, в которых требуется доказать непрерывность функции, используя определения по Гейне и по Коши.

Содержание

См. также:

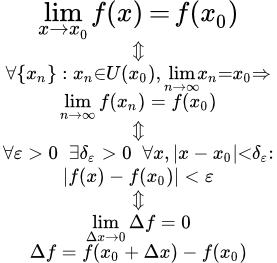
Непрерывность в точке

Определение непрерывности

Непрерывность функции в точке: Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, включая саму точку, и если предел при x стремящемся к x₀ существует и равен значению функции в x₀:
.

Здесь подразумевается, что x₀ – это конечная точка. Значение функции в ней может быть только конечным числом.

Если привлечь сюда определение конечного предела функции в конечной точке, то можно дать развернутую формулировку определения непрерывности функции. Поскольку имеется два равносильных определения предела функции (по Коши и по Гейне), то можно дать, как минимум, еще два эквивалентных определения непрерывности.

Если в определении предела функции в точке , сама точка исключалась из рассмотрения, и мы применяли только проколотые окрестности этой точки, то при определении непрерывности, функция должна быть определена в этой точке и иметь значение, равное предельному. Поэтому при определении непрерывности, можно заменить проколотые окрестности точки простыми окрестностями. Обычно так и делают, хотя никакого противоречия не возникнет, если и при определении непрерывности использовать проколотые окрестности.

Непрерывность функции в точке по Гейне: Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, и если для любой последовательности {x_n}, сходящейся к x₀: , элементы которой принадлежат окрестности U(x₀), последовательность {f(x_n) } сходится к f(x₀):
.
Непрерывность функции в точке по Коши: Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, и если, для любого сколь угодно малого положительного числа ε > 0, существует такое число δ_ε > 0, зависящее от ε, что для всех x, принадлежащих δ_ε - окрестности точки x₀: , значения функции принадлежат ε - окрестности точки f(x₀):
.

Запишем эти определения с помощью логических символов существования и всеобщности.
По Гейне:
.
По Коши:
.

Легко видеть, что определение непрерывности отличается от определения предела только тем, что вместо проколотой окрестности точки используется просто окрестность точки, которая содержит . При этом значение предела может быть равным только значению функции в этой точке: .

Можно сформулировать понятие непрерывности в терминах приращений. Для этого мы вводим новую переменную , которая называется приращением переменной x в точке . Далее мы рассматриваем новую функцию:
.
Ее называют приращением функции в точке . Считаем, что она зависит от переменной : . Тогда можно дать еще одно определение.

Непрерывность функции в точке в терминах приращений: Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности этой точки, и если предел приращения этой функции в точке , при , равен нулю:
.

Определение отсутствия непрерывности

Теперь приведем определение того, что функция не является непрерывной в точке .

Определение отсутствия непрерывности функции в точке

Функция

, определенная на некоторой окрестности точки

не является непрерывной в этой точке,
если предела функции при

не существует,
или он не равен значению функции в точке

По Гейне это означает, что существует такая последовательность , для которой предел либо не существует, либо он не равен :
.

По Коши это означает, что существует такое , так что для любого существует , для которого :
.

Непрерывность на концах отрезка

В рассмотренных выше определениях считается, что функция определена на некоторой окрестности слева и справа от точки . Если функция определена на некотором отрезке , то мы можем применять эти определения для внутренних точек отрезка, для которых . Для концов отрезка a и b нужно дать определение односторонней непрерывности, аналогичное определению односторонних пределов.

Непрерывность функции справа (слева): Функция f(x) называется непрерывной справа (слева) в точке x₀, если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x₀ равен значению функции в x₀:
.

Примеры

Все примеры Доказать, что следующие функции непрерывны на своих областях определения:
1) , используя определения непрерывности по Гейне и Коши ⇓;
2) , используя определение непрерывности по Коши ⇓.

Пример 1

Все примеры ⇑ Используя определения по Гейне и Коши доказать, что функция непрерывна для всех x.

Решение

Пусть есть произвольное число. Докажем, что заданная функция непрерывна в точке . Функция определена для всех x. Поэтому она определена в точке и в любой ее окрестности.

Используем определение по Гейне

Используем определение непрерывности по Гейне ⇑. Пусть есть произвольная последовательность, сходящаяся к : . Применяя свойство предела произведения последовательностей имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , то
.
Непрерывность доказана.

Используем определение по Коши

Используем определение непрерывности по Коши ⇑.
Рассмотрим случай . Мы вправе рассматривать функцию на любой окрестности точки . Поэтому будем считать, что
(П1.1) .

Применим формулу:
.
Учитывая (П1.1), сделаем оценку:

;
(П1.2) .

Применяя (П1.2), оценим абсолютную величину разности:
;
(П1.3) .
Вводим положительные числа и , связав их соотношениями:
.
Согласно свойствам неравенств, если выполняется (П1.3), если и если , то .

Это означает, что для любого положительного всегда найдется . Тогда для всех x, удовлетворяющих неравенству , автоматически выполняется неравенство:
.
Это означает, что функция непрерывна в точке .

Теперь рассмотрим точку . В этом случае
.
Вводим положительные числа и :
.

Отсюда видно, что для любого положительного всегда найдется . Тогда для всех x, таких что , выполняется неравенство:
.
Это означает, что функция непрерывна в точке .

Аналогичным способом можно доказать, что функция , где n – натуральное число, непрерывна на всей действительной оси.

Пример 2

Все примеры ⇑ Используя определение непрерывности по Коши ⇑ доказать, что функция непрерывна для всех .

Решение

Заданная функция определена при . Докажем, что она непрерывна в точке .

Рассмотрим случай .
Мы вправе рассматривать функцию на любой окрестности точки . Поэтому будем считать, что
(П2.1) .

Применим формулу:
(П2.2) .
Положим . Тогда
.

Учитывая (П2.1), сделаем оценку:

.
Итак,
.

Применяя это неравенство, и используя (П2.2), оценим разность:

.
Итак,
(П2.3) .

Вводим положительные числа и , связав их соотношениями:
.
Согласно свойствам неравенств, если выполняется (П2.3), если и если , то .

Теперь рассмотрим точку . Нам нужно показать, что заданная функция непрерывна в этой точке справа. В этом случае
.
Вводим положительные числа и :
.

Отсюда видно, что для любого положительного всегда найдется . Тогда для всех x, таких что , выполняется неравенство:
.
Это означает, что . То есть функция непрерывна справа в точке .

Аналогичным способом можно доказать, что функция , где n – натуральное число, непрерывна при .

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов. Опубликовано: 21-08-2018 Изменено: 15-02-2021

См. также: