Теорема Больцано – Коши о промежуточном значении

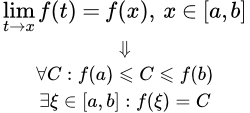
Вторая теорема Больцано – Коши о промежуточном значении

Пусть функция  f  непрерывна на отрезке [a,b].
И пусть C есть произвольное число, находящееся между значениями функции на концах отрезка: A = f(a) и B = f(b).
Тогда существует точка ξ ∈ [a,b], для которой
f(ξ) = C.
Доказательство ⇓

Следствие 1 (первая теорема Больцано – Коши)

Пусть функция непрерывна на отрезке .
И пусть значения функции на концах отрезка имеют разные знаки: или .
Тогда существует точка , значение функции в которой равно нулю:
.

Следствие 2

Пусть функция непрерывна на отрезке .
И пусть .
Тогда функция принимает на отрезке все значения из и только эти значения:
  при  .

Доказательство второй теоремы Больцано – Коши

Формулировка ⇑

Рассмотрим случай .
Разделим отрезок пополам точкой .
Если , то выберем левую половину:
.
В противном случае выберем правую половину:
.
В результате получим отрезок , на котором
.

Отрезок также разделим пополам точкой .
Если , то выберем левую половину:
.
В противном случае выберем правую половину:
.
В результате получим отрезок , на котором
.

Продолжая процесс деления, получаем последовательность вложенных отрезков:
.
Для каждого отрезка выполняются неравенства:
(3.1)   .

Поскольку длина отрезка стремится к нулю, при , то согласно лемме о вложенных отрезках, существует единственная точка , к которой сходятся последовательности и :
(3.2)   .

Рассмотрим последовательности и . Используя (3.2) и учитывая непрерывность функции на отрезке , применим определение непрерывности функции в точке по Гейне. Тогда
(3.3)   .

Рассмотрим неравенства (3.1):
(3.1)   .
Применяя (3.3) и используя свойства пределов последовательностей, связанные с неравенствами, имеем:
, или
.
Отсюда следует, что .

Для случая теорема доказана.
Теперь рассмотрим случай .
Здесь доказательство остается тем же самым, только знаки неравенств меньше или равно нужно заменить на больше или равно:
.

Теорема доказана.