Неравенства и лемма Бернулли
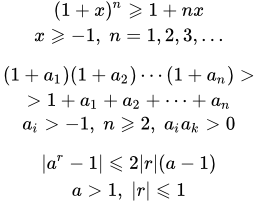
Зачем нужны неравенства Бернулли
Важность неравенств Бернулли заключается в том, что они позволяют сравнить показательную и степенную функции с линейными. Неравенства Бернулли нужны при выводе свойств показательной функции, для нахождения второго замечательного предела (см. «Число e – его смысл и доказательство сходимости последовательности», «Доказательство второго замечательного предела и его следствий»). Второй замечательный предел применяется для вычисления производной показательной функции.
Формулировки неравенств
и натуральном n = 1, 2, 3, ...
имеет место следующее неравенство:
(1 + x)n ≥ 1 + nx.
Оно называется неравенством Бернулли.
Доказательство
При или оно превращается в равенство. Для остальных значений – это строгое неравенство.
.
.
Доказательство
В математическом анализе, при выводе свойств показательной функции, применяется одно из следствий, которое называется леммой Бернулли.
Лемма Бернулли также справедлива и для действительных r. Выпишем ее еще раз, изменив обозначения.
Доказательства неравенств
Неравенство Бернулли
Все неравенства При x ≥ –1и натуральном n = 1, 2, 3, ...
имеет место следующее неравенство:
(1 + x)n ≥ 1 + nx.
Докажем неравенство методом математической индукции. Выпишем его еще раз:
(1.1) .
1. При неравенство выполняется:
.
2. Предположим, что неравенство (1.1) выполняется для произвольного натурального n.
3. Используя (1.1) докажем, что неравенство выполняется для .
.
Поскольку выполняется (1.1) и , то
.
Здесь мы использовали тот факт, что .
Итак, из (1.1) следует неравенство для :
.
Неравенство доказано.
Более общая форма неравенства Бернулли
Все неравенства Пусть числа одного знака (не равны нулю) и больше, чем –1;.
.
Докажем неравенство методом математической индукции. Выпишем его еще раз:
(2.1) .
1. При неравенство выполняется:
.
Здесь мы учли, что и одного знака и не равны нулю. Поэтому .
2. Предположим, что неравенство (2.1) выполняется для произвольного натурального .
3. Используя (2.1) докажем, что неравенство выполняется для .
Поскольку выполняется (2.1) и , то
.
Здесь мы использовали тот факт, что величины одного знака и не равны нулю. Поэтому их произведения .
Итак, из (2.1) следует неравенство для :
.
Неравенство доказано.
Выпишем неравенство еще раз:
(3.1) , , , .
1. Пусть .
1.1. Пусть , где – натуральное число.
Применим неравенство Бернулли:
, .
Положим . Тогда , , ;
;
(3.2) .
Для лемма доказана.
1.2. Используем (3.2), чтобы доказать лемму для . Для этих значений, всегда можно найти такое натуральное , чтобы выполнялись неравенства:
(3.3) .
Пользуясь тем, что функция строго возрастает, , , и применяя (3.2) и (3.3), имеем:
;
(3.4) .
Для лемма доказана.
2. Пусть .
Заметим, что в этом случае . Тогда можно применить (3.4), переписав его в виде:
.
Также замечаем, что , . Тогда
.
Для лемма доказана.
3. Пусть .
Тогда , и (3.1) превращается в равенство.
Лемма доказана.
Выпишем неравенство еще раз:
(4.1) , .
Выше мы доказали лемму Бернулли ⇑ для рациональных x:
(3.1) , , , .
Воспользуемся этим результатом для обобщения на область действительных чисел.
Возьмем произвольную последовательность рациональных чисел , сходящуюся к действительному числу x, элементы которой принадлежат отрезку . Тогда
.
Для элементов этой последовательности выполняется лемма Бернулли (3.1):
(4.2) .
Выполняем предельный переход .
Применяя арифметические свойства пределов последовательностей и определение показательной функции, имеем:
;
.
Применяем к (4.2) свойство пределов последовательностей, связанных неравенством:
;
.
Лемма доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
