Определение и свойства показательной функции
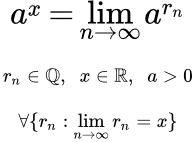
Определение показательной функции
Определение на множестве натуральных чисел
- Показательная функция, зависящая от натурального аргумента
- Показательная функция f(n) = an, с основанием a, от натурального аргумента n – это произведение n множителей, каждый из которых равен a:
.
Здесь .
При она обладает следующими свойствами, вытекающих из правил умножения чисел:
(1.1) a x > 0 при a > 0;
(1.2) строго возрастает при a > 1 и строго убывает при 0 < a < 1;
(1.3) ;
(1.4) ;
(1.5) .
Определение на множестве целых чисел
Если положить:
(1.6) ,
(1.7) ,
то показательная функция становится определенной и для целых чисел. При этом свойства (1.1) – (1.5) по прежнему выполняются, в которых , . Подробнее ⇓
Определение на множестве рациональных чисел
Если положить:
(1.8) ,
где , то показательная функция становится определенной и для рациональных чисел . При этом выполняются свойства (1.1) - (1.7). В них , . Подробнее ⇓
Определение на множестве действительных чисел
Далее, основываясь на свойствах показательной функции (1.1) - (1.8), определенной на множестве рациональных чисел, мы определяем эту функцию на множестве действительных чисел и даем доказательство ее свойств.
Лемма Пусть последовательность рациональных чисел сходится к действительному числу x:
.
И пусть a > 0. Тогда существует предел последовательности :
,
и этот предел может зависеть от числа x, но не зависит от последовательности .
Доказательство ⇓
- Показательная функция
- Пусть a > 0; a, x ∈ ℝ.
Показательная функция f(x) = ax с основанием a – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.
Это определение справедливо и в случае, если x является рациональным числом. При этом совпадает со значением показательной функции, определяемом на множестве рациональных чисел. Чтобы убедиться в этом, достаточно в качестве последовательности взять последовательность с постоянными членами .
Теорема. Свойства показательной функции
(R.0) определена, при , для всех
(R.1) при a ≠ 1 имеет множество значений ;
(R.2) строго возрастает при , строго убывает при , является постоянной при ;
(R.3) ;
(R.3*) ;
(R.4) ;
(R.5) ;
(R.5*) ;
(R.6) ;
(R.7) ;
(R.8) непрерывна для всех ;
(R.9) при ;
при .
Доказательство
Доказательства
Доказательства свойств на множестве целых чисел
Исследуем вопрос – что будет, если для функции, обладающей свойствами (1.3) – (1.5), присвоить отрицательные значения аргумента? Положим
.
Умножим это уравнение на и воспользуемся свойством (1.3):
.
Поскольку , то мы получаем:
.
Отсюда , или
.
В частности, .
Таким образом, свойства (1.3) – (1.5) выполняются для отрицательных и нулевого значения n, если положить:
;
.
Тем самым мы определили значения показательной функции для целых чисел. Однако это возможно не для всех значений основания a. Поскольку деление на нуль не возможно, то .
Доказательства свойств на множестве рациональных чисел
Теперь рассмотрим вопрос об определении показательной функции для рациональных значений аргумента. Пусть есть рациональное число. Его можно представить в виде дроби:
,
где – целое, – натуральное.
Возьмем самый простой случай. Пусть . Рассмотрим уравнение:
.
Умножим его левую и правую части на себя n раз. То есть возведем в степень n и применим свойство (1.4):
;
(Q.1) .
Таким образом, есть корень степени n из a:
.
Для любого и для , существует единственное решение уравнения (Q.1) в области действительных чисел (см. «Доказательство существования и единственности корня степени n»).
Далее мы используем свойства корней:
(Q.2) ;
(Q.3) .
(Q.4) .
(Q.5) .
Свойство (Q.2) выполняется при . Покажем, что оно также справедливо и при . При доказательстве мы будем использовать (1.1) – (1.7) для целых значений x и свойства (Q.2) – (Q.5) с для корней.
Пусть . Тогда
.
Итак, (Q.2) справедливо и для . То есть оно выполняется для целых m и натуральных n.
В силу свойства (Q.2), мы можем определить значения показательной функции для рациональных значений аргумента:
.
Используя свойства (1.3) – (1.5) для целых значений аргумента и свойства корней (Q.2) – (Q.4), можно доказать, что (1.3) – (1.5) выполняются и для рациональных значений аргумента показательной функции.
Докажем свойство (1.3). Поскольку x и y рациональные, то их можно выразить через целые и натуральные числа: . Тогда
.
Докажем свойство (1.4).
.
Докажем свойство (1.5). Пусть . Тогда
.
Доказательство леммы
Лемма
Пусть последовательность рациональных чисел сходится к действительному числу x:
.
И пусть a > 0. Тогда существует предел последовательности :
,
и этот предел может зависеть от числа x, но не зависит от последовательности .
Доказательство
1. Докажем существование предела
.
Поскольку последовательность сходится, то для нее выполняется условие Коши. Это означает, что имеется такая функция , при которой для любого выполняется неравенство:
(Л.1) при .
1.1. Пусть .
Докажем, что условие Коши выполняется для последовательности .
Подставим в (Л.1) . Тогда
(Л.2) при .
Применим лемму Бернулли. При имеем:
(Л.3) .
Поскольку последовательность сходится к конечному числу, то она ограничена некоторым числом :
для всех n.
Поскольку показательная функция, определенная на множестве рациональных чисел строго возрастает при a > 1, то
для всех m.
Обозначим . В силу свойства (1.1), . Подставим в (Л.3) и применим условие Коши (Л.1). При имеем:
.
Если положить , то
при .
Итак, мы нашли такую функцию , при которой для любого ,
при .
То есть выполняется условие Коши для последовательности . Тогда на основании критерия Коши, эта последовательность сходится.
1.2. Теперь рассмотрим случай . Сведем его к предыдущему. Положим . Тогда , . Мы доказали, что последовательность сходится. Единицу в числителе можно рассматривать как элемент последовательности с постоянными членами, равными 1. Тогда, на основании арифметических свойств, существует предел частного последовательностей .
2. Теперь докажем, что предел не зависит от выбора последовательности .
Пусть мы имеем две, сходящиеся к x, последовательности и :
.
Мы доказали, что существуют пределы
и .
Теперь нам нужно доказать, что .
Составим последовательность так, чтобы последовательности и являлись ее подпоследовательностями. Для нечетных n, положим ; для четных: . Последовательность имеет предел . Тогда, согласно доказанному выше, существует предел . Далее замечаем, что последовательности и являются подпоследовательностями последовательности . Поскольку предел любой подпоследовательности равен пределу последовательности, то
.
Лемма доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
