О большое и о малое. Сравнение функций

Даны определения о малого, о большого, эквивалентных (асимптотически равных) функций, функций одного порядка, и их свойства. Приводятся доказательства свойств и теорем. Эти свойства и теоремы используются для сравнения функций и вычисления пределов при аргументе, стремящемся к конечной или бесконечно удаленной точке.

Содержание

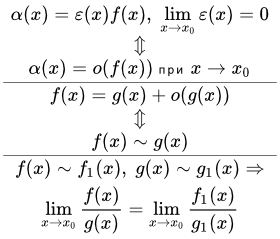
Определения

о малое: Символом о малое обозначают любую бесконечно малую функцию o(f(x)) по сравнению с заданной функцией f( x) при аргументе, стремящемся к некоторому конечному или бесконечному числу x₀.
Бесконечно малая по сравнению с функцией: Функция α называется бесконечно малой по сравнению с функцией f при :
при
(читается: « есть о малое от при »),
если существует такая проколотая окрестность точки , на которой
при ,
где – бесконечно малая функция при :
.
Бесконечно малая более высокого порядка: Если, в предыдущем определении, f является бесконечно малой функцией при , то говорят, что является бесконечно малой более высокого порядка, чем f при .

Заметим, что просто бесконечно малая функция при является бесконечно малой по сравнению с постоянной функцией, не равной нулю.

О большое: Первое определение
Символом О большое обозначают любую функцию , ограниченную относительно функции при аргументе, стремящемся к некоторому конечному или бесконечному числу x₀.
Второе определение
при ,
если на некоторой проколотой окрестности точки ,
,
где – функция, которая определена и ограничена на этой окрестности.
Функция, ограниченная относительно функции: Функция f ограничена относительно функции g при x → x₀,
пишется при ,
читается « есть О большое от при »,
если функции f и g определены на некоторой проколотой окрестности точки и существует такое число C, что на этой окрестности выполняется неравенство:
.
Здесь x₀ ∈ ℝ. Окрестность может быть как двусторонней, так и односторонней. В последнем случае пишут x → x₀ ± 0 или x → ±∞.

Просто ограниченная, на некоторой проколотой окрестности точки , функция является ограниченной по сравнению с постоянной функцией, не равной нулю.

Функции одного порядка: Функции f и g называются функциями одного порядка при :
при ,
если и при .
Это определение также можно записать так:
.
При этом функции и определены и ограничены на некоторой проколотой окрестности точки .
Эквивалентные, асимптотически равные функции: Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.
Главная часть функции: Если
.
то говорят, что является главной частью при . Главная часть определена не однозначно. Любая эквивалентная функция является главной частью к исходной.

Подчеркнем, что означает одну из функций, принадлежащей множеству бесконечно малых функций по сравнению с . Или это функция, о которой известно, что она является бесконечно малой. Другие свойства , в конкретном применении, не представляют интереса. Например, выражение означает, что если прибавить одну функцию из множества бесконечно малых (по сравнению с ) функций к другой функции из того же множества, то их сумма является функцией, которая также принадлежит этому множеству. Выражение означает, что , то есть что принадлежит множеству функций, бесконечно малых по сравнению с .

Определения в компактном виде

Приведенные выше определения можно дать в однообразном компактном виде.
при ;
при ;
при ;
при .

Свойства и теоремы

Теорема. Свойства о малого

1) Если , то при .
2) Если на некоторой проколотой окрестности точки , при ,
и , то
.
Пусть на некоторой проколотой окрестности точки определены функции и . Тогда при выполняются следующие соотношения.
3.1) , где c ≠ 0 – постоянная.
3.2) ;
3.3) ;
3.4) ;
3.5) , где .
Доказательство ⇓

Свойства о малого, применяемые в степенных рядах

Здесь m и n – натуральные числа, .
;
;
, если ;
;
;
;
, где ;
, где c ≠ 0 – постоянная;
.

Для доказательства этих свойств нужно выразить о малое через бесконечно малую функцию:
, где .

Свойства О большого

Пусть на некоторой проколотой окрестности точки определены функции и . Тогда при выполняются следующие соотношения;
, где c ≠ 0 – постоянная;
;
;
;
, где .

Доказательства этих свойств аналогичны доказательствам свойств о малого ⇓.

Свойства эквивалентных функций

1) Свойство симметрии. Если, при , , то .
2) Свойство транзитивности. Если, при , и , то .
3) Если , то при .
Доказательство ⇓

Теорема о связи эквивалентных функций с о малым

Для того чтобы две функции и были эквивалентными (или асимптотически равными), необходимо и достаточно чтобы при выполнялось условие:
.
Доказательство ⇓

Это свойство часто записывают так:
.
При этом говорят, что является главной частью при . При этом главная часть определена не однозначно. Любая эквивалентная функция является главной частью к исходной.
В силу свойства симметрии:
.

Теорема о замене функций эквивалентными в пределе частного

Если, при , и и существует предел
, то существует и предел
.
Доказательство ⇓

В силу свойства симметрии эквивалентных функций, если не существует один из этих пределов, то не существует и другой.

Поскольку любая функция, определенная на некоторой проколотой окрестности точки , эквивалентна самой себе, то существуют пределы
.

Заменив функции g и g₁ на 1/g и 1/g₁, получим аналогичную теорему для произведения.
Если, при , и , то
.
Это означает, что если существует один предел, то существует и другой. Если не существует один из этих пределов, то не существует и второй.

Лемма. Признак функций одного порядка

Если существует конечный ненулевой предел
,
то функции f и g одного порядка при :
при .
Доказательство ⇓

Доказательство свойств и теорем

Теорема. Свойства о малого

Все свойства ⇑ 1) Если , то при .

Доказательство

Пусть . Это означает, что существует такая проколотая окрестность точки , на которой определено отношение и поэтому . Тогда на этой окрестности
,
где . По условию
.
Тогда .
Свойство 1) доказано.

2) Если на некоторой проколотой окрестности точки , при ,
и , то
.

Доказательство

Поскольку , то на рассматриваемой проколотой окрестности точки ,
.
Поскольку , то
.
Свойство 2) доказано.

Пусть на некоторой проколотой окрестности точки определены функции и . Тогда при выполняются следующие соотношения.
3.1) , где c ≠ 0 – постоянная.
3.2) ;
3.3) ;
3.4) ;
3.5) , где .

Доказательство

3.1). Пусть . Согласно определению о малого,
,
где . Введем функцию . Тогда
.
Поскольку , то
.
Свойство 3.1) доказано.

3.2). Докажем, что .
Пусть . Согласно определению о малого,
,
где .
Тогда ,
где . Поскольку
, то
.
Свойство 3.2) доказано.

3.3). Докажем, что .
Пусть . Согласно определению о малого,
,
где . Тогда
.
Здесь . Поскольку
,
то .
Свойство 3.3) доказано.

3.4). Докажем, что .
Пусть . Согласно определению о малого,
,
где ,
.
Согласно арифметическим свойствам предела функции,
.
Тогда .
Свойство 3.4) доказано.

3.5). Пусть при . Тогда, согласно определению о малого, ,
где . Тогда
,
где .
Поскольку и , то
.
Здесь мы воспользовались свойствами степенной функции, ее непрерывностью, теоремой о пределе непрерывной функции от функции и теоремой о пределе абсолютного значения функции.
Свойство 3.5) доказано.

Эквивалентные функции

Свойства эквивалентных функций

Все формулировки ⇑ 1) Свойство симметрии. Если, при , , то .

Доказательство

Поскольку при , , то согласно определению эквивалентной функции, существует такая проколотая окрестность точки , на которой
,
где .
Поскольку функция имеет отличный от нуля предел, то по теореме об ограниченности снизу функции, имеющей ненулевой предел, существует такая проколотая окрестность точки , на которой . Поэтому на этой окрестности . Следовательно, на ней определена функция . Тогда
.
Согласно теореме о пределе частного двух функций,
.
Свойство доказано.

2) Свойство транзитивности. Если, при , и , то .

Доказательство

Поскольку

, то

, где

. Тогда

, где

.
По теореме о пределе произведения двух функций,

.
Свойство доказано.

3) Если , то при .

Доказательство

Поскольку существует предел

, то существует проколотая окрестность точки

, на которой определено частное

и, следовательно,

. Тогда на этой окрестности

. Поскольку

, то

. В силу свойства симметрии,

.
Свойство доказано.

Теорема о связи эквивалентных функций с о малым

Все формулировки ⇑ Для того чтобы две функции и были эквивалентными (или асимптотически равными), необходимо и достаточно чтобы при выполнялось условие:
.

Доказательство

1. Необходимость. Пусть функции и являются эквивалентными при . Тогда
.
Поскольку , то
.
Тогда .
Необходимость доказана.

2. Достаточность. Пусть при ,
.
Тогда , где . Отсюда
.
Поскольку , то
.
Теорема доказана.

Теорема о замене функций эквивалентными в пределе частного

Все формулировки ⇑ Если, при , и и существует предел
, то существует и предел
.

Доказательство

Пусть, при , и . Тогда
, где
.
Поскольку существует предел , то существует такая проколотая окрестность точки , на которой функция определена и отлична от нуля. Поскольку , то, по теореме об ограниченности снизу функции, имеющей ненулевой предел, существует такая проколотая окрестность точки , на которой и, следовательно, . Тогда существует проколотая окрестность точки , на которой функция определена и отлична от нуля и, следовательно, определено частное :
.
Применяем арифметические свойства предела функции:
.

Теорема доказана.

Признак функций одного порядка

Все формулировки ⇑ Лемма
Если существует конечный ненулевой предел
(Л1.1) ,
то функции f и g одного порядка при :
при .

Доказательство

Поскольку существует предел (Л1.1), то по теореме о пределе абсолютного значения функции, существует предел
.
Тогда согласно определению предела функции по Коши, для любого , существует такая проколотая окрестность точки , на которой
при .

Преобразуем неравенство и подставим :
;
;
(Л1.2) .
Из второго неравенства:
,
или .
Из первого неравенства (Л1.2):
,
или .

Лемма доказана.

Использованная литература.
О. И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
А. М. Дымарский. Лекции по математическому анализу. Часть 1. Москва, МФТИ, 2020.
Л. Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С. М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов. Опубликовано: 15-04-2019 Изменено: 12-07-2021