Определение и доказательство свойств логарифма
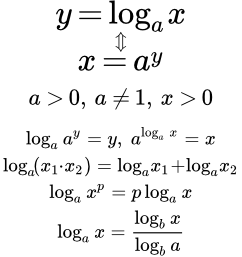
Определение логарифма
- Логарифмическая функция (логарифм)
- с основанием a – это функция, обратная к показательной функции с основанием a. Логарифмическая функция обозначается так:
y = loga x.
Теорема. Свойства логарифма
Логарифмическая функция с основанием a, y = loga xимеет следующие свойства:
(1.1) определена и непрерывна, при и , для положительных значений аргумента,;
(1.2) имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) при ;
(1.7) при ;
(1.8) при ;
(1.9) при .
Доказательство свойств
1.1–1.4. На странице «Определение и доказательство свойств показательной функции» мы доказали, что показательная функция , при , определена, непрерывна и строго возрастает на множестве всех действительных чисел . Она имеет множество значений . Тогда по теореме об обратной функции, на интервале определена, непрерывна и строго возрастает обратная функция, которая называется логарифмом по основанию a. Множество значений логарифма совпадает с областью определения показательной функции и является интервалом .
Случай отличается от рассмотренного выше случая только тем, что для этих значений a, показательная функция строго убывает. Поэтому и обратная функция – логарифм, также строго убывает при .
1.5–1.6. Свойства (1.5–1.6) следуют из определения обратной функции:
для всех ;
для всех .
Полагая , , , , получаем:
для всех x ;
при .
1.7–1.9. Применяем свойства 1.5–1.6 и свойства показательной функции.
;
.
Применяем предыдущее свойство.
;
.
Теорема доказана.
Автор: Олег Одинцов. Опубликовано:
