График обратной функции

График квадратичной параболы и обратной функции - квадратного корня

Доказательство свойства симметрии графиков прямой и обратной функций. Примеры графиков прямых и обратных функций: параболы и корни, степенные функция и логарифмы, тригонометрические функции и обратные к ним. Применение операции сужения функции.

Содержание

См. также:

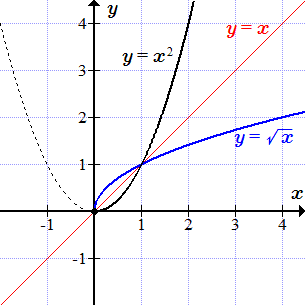
Свойство симметрии графиков обратных функций

Пусть функция f(x) определена на некотором множестве X,
и имеет множество значений Y:

.
И пусть она имеет на множестве X обратную функцию f^-1:

.
Тогда графики прямой

и обратной

функций, построенные при значениях их аргументов

, соответственно, симметричны относительно прямой

Доказательство

Пусть – произвольная точка графика прямой функции , с аргументом, принадлежащим множеству X:
(1) .
Построим точку , симметричную точке относительно прямой , и выразим ее координаты через координаты точки A.

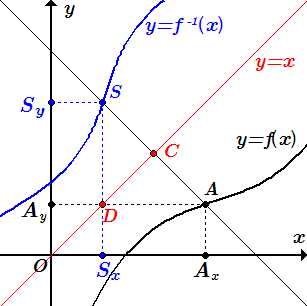
Симметрия графиков прямой и обратной функций — График обратной функции y = f^–1(x) симметричен графику прямой функции y = f(x) относительно прямой y = x.

Для этого через точку A проводим прямую, перпендикулярную прямой . Пусть C – точка пересечения этих прямых. Далее, на проведенной прямой, откладываем точку S, симметричную точке A относительно прямой . При этом
;
.

Из точек A и S опустим перпендикуляры на оси координат. Поскольку прямая составляет угол с осями координат, то и перпендикулярная ей прямая AS также составляет угол с осями координат. Тогда и пересекутся в точке D, принадлежащей прямой . При этом углы у оснований треугольников DAC и SDC равны . По этой причине они являются равнобедренными. А поскольку , то они конгруэнтны. Тогда , и, следовательно,
(2) .

В треугольниках и углы при вершинах O и D равны , а при вершинах равны . Поэтому они равнобедренные и подобные. А поскольку они имеют общее основание OD, то они конгруэнтны. Тогда
(3) .

Используя (2) и (3) имеем:
;
.
Итак, мы выразили координаты симметричной точки S через координаты точки A:
(4) ;
(5) .

Поскольку точка принадлежит графику функции f, то ее координаты связаны уравнением:
(1) .
Поскольку, по условию, f имеет обратную функцию, то
.
Подставляя (4) и (5) находим:
.
То есть мы получили, что симметричная точка S принадлежит графику обратной функции.

Так как мы выбрали точку A произвольно, то это относится ко всем точкам графика .
Все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику обратной функции .
Далее мы можем поменять и местами. В результате получим, что
все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику функции .
Отсюда следует, что графики функций и симметричны относительно прямой .

Свойство доказано.

Примеры графиков обратных функций

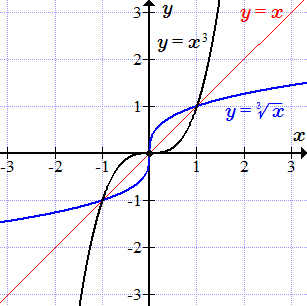
Некоторые функции являются непрерывными и строго монотонными на всей области определения. Поэтому они имеют обратные функции, и их графики симметричны относительно прямой . Например, кубическая парабола строго возрастает для всех x. Поэтому она имеет обратную функцию , график которой симметричен графику параболы относительно прямой .

Существуют функции, которые не являются монотонными на всей области определения. Однако можно указать интервал X, на котором такая функция определена, непрерывна и строго монотонна. В этом случае можно выполнить операцию сужения функции на множество X: . То есть рассматривать только значения аргумента, принадлежащие интервалу X. Тогда на этом интервале она будет иметь обратную функцию. В результате графики суженной функции и обратной функции будут симметричны относительно прямой .

Например, квадратичная парабола, , определена и непрерывна для всех x, но не является монотонной. Но она строго возрастает при , то есть на множестве . Тогда сужение параболы имеет обратную функцию . Их графики симметричны относительно прямой .

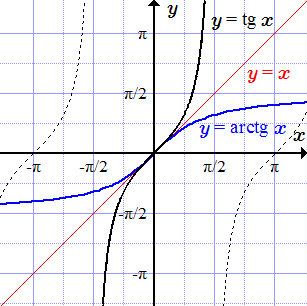
Тригонометрическая функция также не является монотонной, но она непрерывна и строго возрастает при . Тогда ее сужение имеет обратную функцию . Их графики также симметричны относительно прямой .

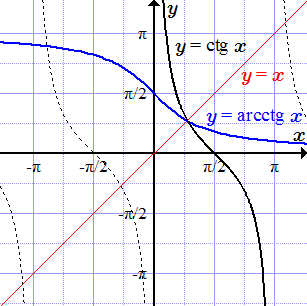
Ниже приводятся графики некоторых элементарных функций. Для некоторых из них выполнена операция сужения, и построен график обратной функции.

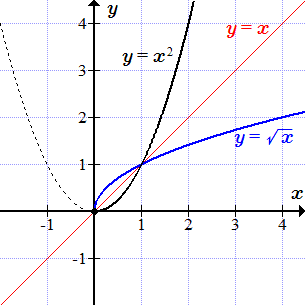
Графики x в квадрате и корень из x — График параболы y = x² и обратной функции – квадратного корня y = √x.

График кубической параболы и кубического корня — График кубической параболы y = x³ и обратной функции – кубического корня y = √3x.

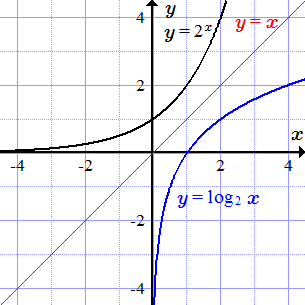
Графики 2 в степени x и логарифм по основанию 2 — График показательной функции с основанием 2, y = 2^x и обратной функции – логарифма с основанием 2, y = log₂ x.

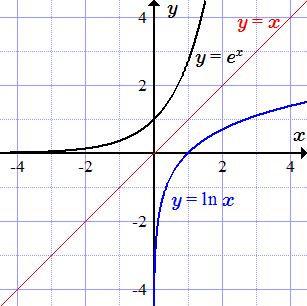
Графики экспонента и натуральный логарифм — График экспоненты y = e^x и обратной функции – натурального логарифма y = ln x.

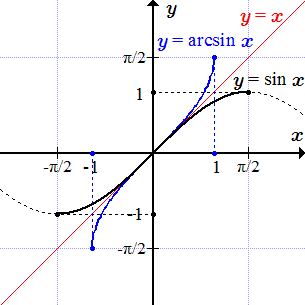
Графики sin(x) и arcsin(x) — График синуса y = sin x и обратной функции – арксинуса y = arcsin x.

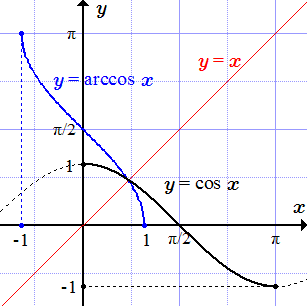
Графики cos(x) и arccos(x) — График косинуса y = cos x и обратной функции – арккосинуса y = arccos x.

Графики tg(x) и arctg(x) — График тангенса y = tg x и обратной функции – арктангенса y = arctg x.

Графики ctg(x) и arcctg(x) — График котангенса y = ctg x и обратной функции – арккотангенса y = arcctg x.

Автор: Олег Одинцов. Опубликовано: 10-12-2020

См. также: