Логарифм - свойства, формулы, график
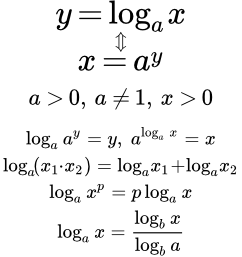
Определение логарифма
- Логарифм с основанием a
- – это функция y(x) = loga x, обратная к показательной функции с основанием a: x(y) = a y.
В дальнейшем будем считать, что основание логарифма a положительное, не равное единице число: .
- Десятичный логарифм
- – это логарифм по основанию числа 10: lg x ≡ log10 x.
- Натуральный логарифм
- – это логарифм по основанию числа e: ln x ≡ loge x.
2,718281828459045...;
.
Графики логарифма
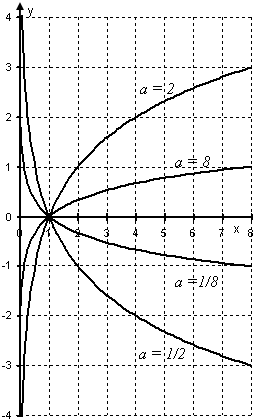
График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. Слева изображены графики функции y = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0 < a < 1 логарифм монотонно убывает.
Свойства логарифма
См. также «Определение и доказательство свойств логарифма».
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
| Область определения | 0 < x < + ∞ | 0 < x < + ∞ |
| Область значений | – ∞ < y < + ∞ | – ∞ < y < + ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
| + ∞ | – ∞ | |
| – ∞ | + ∞ |
Частные значения
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
Логарифм по основанию e называется натуральным логарифмом:
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
- Логарифмирование
- – это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.
- Потенцирование
- – это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.
Доказательство основных формул логарифмов
Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.
Рассмотрим свойство показательной функции
.
Тогда
.
Применим свойство показательной функции
:
.
Докажем формулу замены основания.
;
.
Полагая c = b, имеем:
Обратная функция
Обратной для логарифма по основанию a является показательная функция с показателем степени a.
Если , то
Если , то
Производная логарифма
Производная логарифма от модуля x:
.
Производная n-го порядка:
.
Вывод формул > > >
Для нахождения производной логарифма, его нужно привести к основанию e.
;
.
Интеграл
Интеграл от логарифма вычисляется интегрированием по частям: .
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z:
.
Выразим комплексное число z через модуль r и аргумент φ:
.
Тогда, используя свойства логарифма, имеем:
.
Или
Однако, аргумент φ определен не однозначно. Если положить
, где n - целое,
то будет одним и тем же числом при различных n.
Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
