Показательная функция – свойства, графики, формулы

Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.

Содержание

См. также:

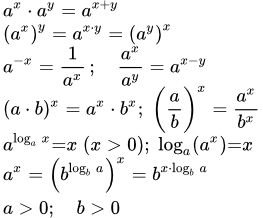
Определение

Показательная функция: – это обобщение произведения n чисел, равных a:
y(n) = aⁿ = a·a·a···a,
на множество действительных чисел x:
y(x) = a^x.
Здесь a – фиксированное действительное число, которое называют основанием показательной функции.
Показательную функцию с основанием a также называют экспонентой по основанию a.

Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3,..., показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (см. ниже ⇓), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где – произвольная последовательность рациональных чисел, сходящаяся к x: .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x.

Строгая математическая формулировка определения показательной функции и доказательство ее свойств приводится на странице «Определение и доказательство свойств показательной функции».

Свойства показательной функции

Показательная функция y = a^x, имеет следующие свойства на множестве действительных чисел ():
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .

Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:

При b = e, получаем выражение показательной функции через экспоненту:

Частные значения

, , , , .

Графики показательной функции

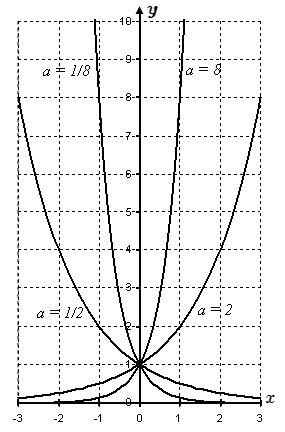
На рисунке представлены графики показательной функции
y(x) = a^x
для четырех значений основания степени: a = 2, a = 8, a = 1/2 и a = 1/8. Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a, тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a, тем сильнее убывание.

Возрастание, убывание

Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

	y = a^x, a > 1	y = a^x, 0 < a < 1
Область определения	– ∞ < x < + ∞	– ∞ < x < + ∞
Область значений	0 < y < + ∞	0 < y < + ∞
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	нет	нет
Точки пересечения с осью ординат, x = 0	y = 1	y = 1
	+ ∞	0
	0	+ ∞

Обратная функция

Обратной для показательной функции с основанием степени a является логарифм по основанию a.

Если , то
.
Если , то
.

Дифференцирование показательной функции

Для дифференцирования показательной функции, ее основание нужно привести к числу e, применить таблицу производных и правило дифференцирования сложной функции.

Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных:
.

Пусть задана показательная функция:
.
Приводим ее к основанию e:

Применим правило дифференцирования сложной функции. Для этого вводим переменную

Тогда

Из таблице производных имеем (заменим переменную x на z):
.
Поскольку – это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.

Производная показательной функции

.
Производная n-го порядка:
.
Вывод формул > > >

Пример дифференцирования показательной функции

Найти производную функции
y = 3^5x

Решение

Выразим основание показательной функции через число e.
3 = e^{ln 3}
Тогда
.
Вводим переменную
.
Тогда

Из таблицы производных находим:
.
Поскольку 5ln 3 – это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.

Ответ

Интеграл

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z:
f(z) = a^z
где z = x + iy; i² = – 1.
Выразим комплексную постоянную a через модуль r и аргумент φ:
a = r e^{i φ}
Тогда

.
Аргумент φ определен не однозначно. В общем виде
φ = φ₀ + 2πn,
где n – целое. Поэтому функция f(z) также не однозначна. Часто рассматривают ее главное значение
.

Разложение в ряд

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов. Опубликовано: 21-02-2014 Изменено: 19-11-2018

См. также: