Теорема о существовании и монотонности обратной функции

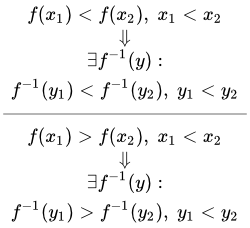
Теорема

Доказательство

Пусть функция  f (x) имеет область определения X и множество значений Y.

Докажем, что она имеет обратную функцию.
Исходя из определения, нам нужно доказать, что
 f (x₁) ≠  f (x₂) для всех x₁ ≠ x₂,  x₁, x₂ ∈ X.
Допустим противное. Пусть существуют числа x₁ ≠ x₂,  x₁, x₂ ∈ X, так что  f (x₁) =  f (x₂). Пусть при этом x₁ < x₂. Иначе, поменяем обозначения, чтобы было x₁ < x₂. Тогда, в силу строгой монотонности  f, должно выполняться одно из неравенств:
 f (x₁) <  f (x₂), если  f  строго возрастает;
 f (x₁) >  f (x₂), если  f  строго убывает.
То есть  f (x₁) ≠  f (x₂). Возникло противоречие. Следовательно, f имеет обратную функцию  f ^–1.

Пусть функция  f  строго возрастает.
Докажем, что и обратная функция также строго возрастает. Введем обозначения:
y₁ =  f (x₁),  y₂ =  f (x₂). То есть нам нужно доказать, что если y₁ < y₂, то x₁ < x₂.

Допустим противное. Пусть y₁ < y₂, но x₁ ≥ x₂.

Если x₁ = x₂, то y₁ =  f (x₁) =  f (x₂) = y₂. В этом случае y₁ = y₂. Возникло противоречие, поскольку, по предположению, y₁ < y₂. Этот случай отпадает.

Пусть x₁ > x₂. Тогда, в силу строгого возрастания функции  f ,  f (x₁) >  f (x₂), или y₁ > y₂. Возникло противоречие. Поэтому возможен только случай x₁ < x₂.
Для строго возрастающей функции лемма доказана.

Пусть функция  f  строго убывает.
Докажем, что и обратная функция также строго убывает. Нам нужно доказать, что если y₁ < y₂, то x₁ > x₂.

Допустим противное. Пусть y₁ < y₂, но x₁ ≤ x₂.

Если x₁ = x₂, то y₁ =  f (x₁) =  f (x₂) = y₂. В этом случае y₁ = y₂. Возникло противоречие, поскольку, по предположению, y₁ > y₂.

Пусть x₁ < x₂. Тогда, в силу строгого убывания функции  f ,  f (x₁) >  f (x₂), или y₁ > y₂. Возникло противоречие. Поэтому возможен только случай x₁ > x₂.

Теорема доказана.