Непрерывность и свойства степенной функции
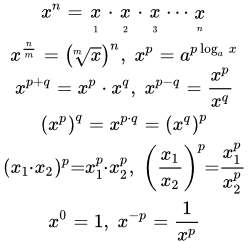
Определение степенной функции
- Степенная функция
- с показателем степени p – это функция f(x) = x p, значение которой в точке x равно значению показательной функции с основанием x в точке p.
Кроме этого, f(0) = 0 p = 0 при p > 0.
Степенную функцию можно выразить через показательную и логарифм:
.
В качестве основания a можно взять любое действительное число . В математическом анализе наиболее удобно использовать число e:
2,718281828459045....
Тогда ,
.
Выше мы представили степенную функцию как сложную, составленную из логарифмической и показательной функций. Поэтому ее свойства можно получить из свойств этих функций.
Свойства степенной функции
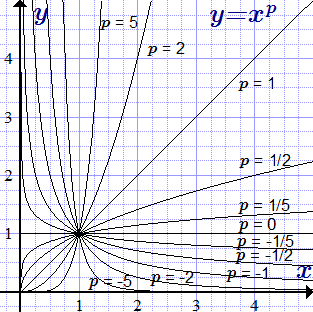
Здесь мы рассмотрим свойства степенной функции y = x p при неотрицательных значениях аргумента . Для рациональных , при нечетных m, степенная функция определена и для отрицательных x. В этом случае, ее свойства можно получить, используя четность или нечетность. Так, при четных функция четна:
.
При нечетных – нечетна:
.
Эти случаи подробно рассмотрены и проиллюстрированы на странице «Степенная функция, ее свойства и графики».
Теорема. Свойства степенной функции (x ≥ 0)
Степенная функция, y = x p, с показателем pимеет следующие свойства:
(1.1) определена и непрерывна на множестве
при ,
при ;
(1.2) имеет множество значений
при ,
при ;
(1.3) строго возрастает при ,
строго убывает при ;
(1.4) при ;
при ;
(1.5) ;
(1.5*) ;
(1.6) ;
(1.7) ;
(1.7*) ;
(1.8) ;
(1.9) .
Доказательство свойств
Для доказательства свойств, представим степенную функцию как сложную:
(2) .
Используем следующие обозначения:
(3) , где .
В качестве a возьмем произвольное число . При доказательстве будем использовать свойства показательной функции и логарифмической.
1.1. Найдем область определения. Логарифмическая функция определена при . Показательная функция определена для всех t. Поэтому степенная функция (2) определена при . Кроме этого, согласно определению, при , степенная функция определена в точке .
Исследуем на непрерывность. Поскольку логарифм и показательная функция непрерывны на своих областях определения, то, по теореме о непрерывности сложной функции, степенная функция непрерывна при .
Рассмотрим случай . Покажем, что показательная функция непрерывна в точке слева. Применяя теорему о пределе сложной функции, имеем:
.
Здесь мы использовали общепринятые обозначения:
.
Таким образом, . Непрерывность в точке слева доказана.
1.4. Найдем пределы на границе области определения.
Пусть .
По определению, .
Находим предел при , аналогично предыдущему:
.
Пусть . Тогда
;
.
1.3. Докажем, что степенная функция строго монотонна на области определения.
При , функции и строго возрастают. Поэтому сложная функция также строго возрастает.
Поскольку и при , , то степенная функция строго возрастает на области определения .
При , функция строго убывает, а функция строго возрастает. Поэтому сложная функция строго убывает на области определения .
1.2. Найдем множество значений степенной функции .
Для этого рассмотрим ее на отрезке , где . Поскольку функция на этом отрезке строго монотонна, то она достигает минимума и максимума на его концах – в точках и . Как мы уже доказали, степенная функция непрерывна на своей области определения. Тогда, согласно теореме Больцано – Коши о промежуточном значении, она принимает все значения из отрезка , если и , если . Устремляя и , и используя найденные выше пределы получаем, что множеством значений показательной функции является множество неотрицательных чисел при , и множество положительных чисел при .
Свойства (1.1-4) доказаны.
1.5-9. Доказательство свойств (1.5-9) приводится на странице «Определение и доказательство свойств показательной функции»
Автор: Олег Одинцов. Опубликовано:
