Производные второго и высших порядков – основные формулы, определения и теоремы
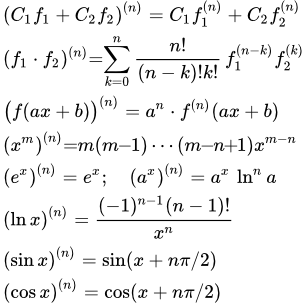
Определения
Поскольку производная сама является функцией от переменной , то можно дать определение производной от производной, которая называется производной второго порядка.
- Производная второго порядка функции
- Пусть для функции , в окрестности некоторой точки , определена ее производная . И пусть имеет производную в этой точке.
Второй производной функции в точке называется производная от первой производной в этой точке:
.
Вторую производную также называют производной второго порядка функции. - Производная n-го порядка функции
- Пусть для функции , в окрестности некоторой точки , определена ее n–1-я производная . И пусть функция имеет производную в этой точке.
n-й производной функции в точке называется производная от n-1-й производной в этой точке:
.
n-ю производную также называют производной n-го порядка функции или производной порядка n функции. - n раз дифференцируемая функция
- n раз дифференцируемой функцией на множестве X называется функция, имеющая в каждой точке множества X производную n-го порядка (и, следовательно, имеющая производные всех порядков меньших n).
Обозначения
Производная функции второго порядка может обозначаться так:
.
Третьего порядка:
.
Для производных более высоких порядков вместо штрихов используются римские цифры. Например, для четвертого порядка:
.
Для произвольного n-го порядка:
.
При этом стоит иметь в виду, что обозначение является принятым сокращением, под которым подразумевают следующее:
.
Арифметические свойства
Теорема. Высшие производные суммы функций
Пусть функции и имеют производные n–го порядка в точке .И пусть и – постоянные, не зависящие от величины.
Тогда любая функция вида
(1)
имеет в точке n–ю производную:
.
Для доказательства нужно продифференцировать (1) n раз, применяя правило вынесения постоянной за знак производной и формулу производной суммы функций.
При получаем правило вынесения постоянной за знак n-ой производной:
.
Теорема. Высшие производные произведения функций (формула Лейбница)
Пусть функции и имеют производные n–го порядка в точке .Тогда произведение функций
(2)
имеет в точке n–ю производную, которая определяется по формуле:
.
Эту формулу также можно выразить через биномиальные коэффициенты :
.
Здесь подразумевается, что .
Доказательство формулы Лейбница двумя способами
В более общем случае произведения m функций, формула Лейбница имеет следующий вид:
.
Суммирование ведется по всем возможным целым неотрицательным значениям , сумма которых равна n.
Высшие производные частного функций
Для частного функций
(3)
нет такой формулы, позволяющей находить высшие производные в общем виде. Их можно находить последовательным дифференцированием, применяя формулу производной частного, либо рассматривая дробь как произведение двух функций . Также можно умножить (3) на , и последовательно вычислять производные, дифференцируя произведения:
;
;
;
· · ·
Высшие производные сложной функции
Здесь мы получим формулу, которая имеет применение при дифференцирования одного распространенного частного случая сложной функции:
(4) .
Производная в левой части берется по переменной ; производная – по аргументу функции .
Рассмотрим сложную функцию
(5) .
Введем переменную . Тогда (5) можно представить в следующем виде:
, где .
Найдем ее производную, применяя правило дифференцирования сложной функции:
;
(6) .
Дифференцируя (6), находим вторую производную.
;
;
.
Здесь функции и зависят от переменной . Поэтому их производные по умолчанию берутся по . Функция зависит от . Поэтому и ее производная – по переменной . Опуская лишние индексы, получим более короткую запись:
.
Третья производная:
;
.
Если продолжим, то получим более громоздкие формулы. Разберем только один важный случай, когда функция линейна по переменной , то есть определяется по формуле:
,
где и – постоянные. Тогда ; и все производные от второго и более высоких порядков равны нулю. Поэтому выражение для производной произвольного n-го порядка имеет вид:
.
Эту формулу можно представить в более удобном для восприятия виде:
.
Подчеркнем, что производная в левой части берется по переменной . Производная в правой части – по аргументу функции , то есть по , а не по .
Формулы производных высших порядков элементарных функций
При вычислении производных часто используют следующие формулы производных n-го порядка.
степенной функции
показательной функции
натурального логарифма
синуса
косинуса
Применяя (4), эти формулы n-х производных по переменной x можно переписать так:
;
;
;
;
.
Производные высших порядков некоторых элементарных функций имеют довольно громоздкий вид. Далее приводятся их формулы для справок.
, где тангенса
, где котангенса
,
где – многочлен степени . Он определяется по формулам:
;
.
Здесь
арксинуса и арккосинуса
арктангенса и арккотангенса
Использованная литература:
А.М. Тер-Крикоров, М.И. Шабунин. Курс математического анализа. Москва, ФИЗМАТЛИТ, 2001.
Автор: Олег Одинцов. Опубликовано:
