Вывод производных высших порядков арксинуса (arcsin x) и арккосинуса (arccos x)

Представлен вывод производных высших порядков арксинуса (arcsin x). Формулы производных арксинуса второго, третьего, четвертого и пятого порядка. Производная n-го порядка выражается через многочлен и корень. Даны уравнения для многочленов и вывод значений их коэффициентов. Выражение производной n-го порядка арккосинуса через производную арксинуса.

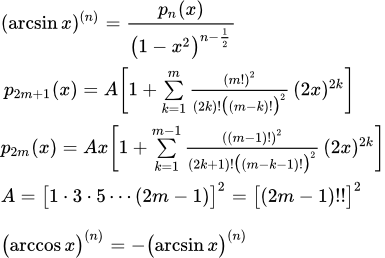
Основные результаты

Рассмотрим функцию арксинус от переменной x:
(1)   y = arcsin x.
Нам известна производная первого порядка этой функции (см. Вывод производных арксинуса и арккосинуса):
(2)   y^′ = 1√ 1 – x² .

Непосредственным дифференцированием, или используя приведенные ниже формулы, можно найти производные арксинуса от второго до пятого порядков:
y^′′ = x(1 – x²)^3 / 2;   y^′′′ = 1 + 2x²(1 – x²)^5 / 2;   y^IV = 9x + 6x³(1 – x²)^7 / 2;   y^V = 9 + 72x² + 24x⁴(1 – x²)^9 / 2.

В общем случае, производная арксинуса произвольного, n-го порядка, выражается через многочлен и корень:
(3)   y⁽ⁿ⁾ = p_n (x)( 1 – x² )^n – 12,
где p_n (x) – многочлен степени n – 1. Он определяется по формулам:
(4)   p_2m + 1 (x) = A [1 + ^mΣ_k = 1 (m!)²(2k)!( (m – k)! )² (2x)^2k];
(5)   p_2m (x) = Ax [1 + ^m – 1Σ_k = 1 ((m – 1)!)²(2k + 1)!( (m – k – 1)! )² (2x)^2k].
Здесь A = [1 ⋅ 3 ⋅ 5⋅ ⋅ ⋅(2m – 1)]² ≡ [(2m – 1)!!]².

Отсюда можно определить производную арксинуса в нуле, то есть при x = 0. Для нечетных n = 2m + 1,
(arcsin x )^(2m + 1) (0) = [1 ⋅ 3 ⋅ 5⋅ ⋅ ⋅(2m – 1)]² ≡ [(2m – 1)!!]².
Для четных n = 2m, производная равна нулю:
(arcsin x )^(2m) (0) = 0.

Производная n-го порядка арксинуса удовлетворяет дифференциальному уравнению:
(6)   (1 – x²) y^(n + 2) – (2n + 1) xy^(n + 1) – n²  y⁽ⁿ⁾ = 0.
Это уравнение связывает производные трех порядков. При n = 0 получаем уравнение, связывающее производные первого и второго порядков:
(7)   (1 – x²)y^′′ – xy^′ = 0.

Многочлены p_n (x) связаны следующими соотношениями:
(8)   p_n + 1 = (1 – x²) p^′_n + (2n – 1) xp_n;
(9)   p_n + 2 – (2n + 1) xp_n + 1 – n² (1 – x²) p_n = 0;
(10)   (1 – x²) p^′′_n + (2n – 3) xp^′_n – (n – 1)²  p_n = 0.

Производные высших порядков арккосинуса (arccos x)

Зная значения производных арксинуса, легко получить значения производных арккосинуса. Для этого нужно воспользоваться связью между этими функциями:
arccos x = π2 – arcsin x.
Тогда производная n-го порядка арккосинуса равна производной n-го порядка арксинуса, взятой с обратным знаком:
(arccos x )⁽ⁿ⁾ = –(arcsin x )⁽ⁿ⁾.

Вывод формул

Ниже мы выведем формулы (4–5), которые определяют значения коэффициентов многочленов p_n (x). Однако, чтобы сделать это, нам нужно сначала вывести формулы (6–10), устанавливающие связь между производными арксинуса и соотношения между многочленами.

Дифференциальное уравнение, которому удовлетворяют производные арксинуса высших порядков

Пусть
(1)   y = arcsin x.
Производную первого порядка от арксинуса мы уже нашли:
(2)   y^′ = 1√ 1 – x² .
Дифференцируя, находим производную второго порядка:
y^′′ = ( ( 1 – x² )^–1 / 2 )^′ = – 12 ( 1 – x² )^–3 / 2 ⋅ ( 1 – x² )^′ = – 12 ⋅ 1(1 – x²)^3 / 2 ⋅ (–2x);
y^′′ = x(1 – x²)^3 / 2 = x(1 – x²) √ 1 – x² .
Учитывая (2), запишем производную второго порядка в следующем виде:
y^′′ = x1 – x² y^′.
Отсюда получаем дифференциальное уравнение, которому удовлетворяют производные арксинуса первого и второго порядков:
(7)   (1 – x²)y^′′ – xy^′ = 0.

Дифференцируем это уравнение n раз, применяя формулу Лейбница. В результате получаем формулу (6), связывающую производные трех высших порядков:
(1 – x²) y^(n + 2) + n( 1 – x² )^′ y^(n + 1) + n(n – 1)2 ( 1 – x² )^′′ y⁽ⁿ⁾ –
 xy^(n + 1) – n (x)^′ y⁽ⁿ⁾ = 0;
(1 – x²) y^(n + 2) + n (–2x) y^(n + 1) + n(n – 1)2 (–2) y⁽ⁿ⁾ – xy^(n + 1) – ny⁽ⁿ⁾ = 0;
(1 – x²)y^(n + 2) – 2nxy^(n + 1) – (n² – n) y⁽ⁿ⁾ – xy^(n + 1) – ny⁽ⁿ⁾ = 0;
(6)   (1 – x²) y^(n + 2) – (2n + 1) xy^(n + 1) – n²  y⁽ⁿ⁾ = 0.

Выражение производной n-го порядка через многочлен и корень

Легко убедиться, что производная арксинуса n-го порядка имеет следующий вид:
(3)   y⁽ⁿ⁾ = p_n (x)( 1 – x² )^n – 12,
где p_n (x) – многочлен степени n – 1.

Связь между многочленами различных степеней

Выведем формулу (9), устанавливающую связь между многочленами различных степеней. Для этого подставим (3) в (6):
(1 – x²) p_n + 2( 1 – x² )^{n + 2 – 12} – (2n + 1) x p_n + 1( 1 – x² )^{n + 1 – 12} – n² p_n( 1 – x² )^n – 12 = 0.
Умножив на ( 1 – x² )^n + 12, получим (9):
(9)   p_n + 2 – (2n + 1) xp_n + 1 – n² (1 – x²) p_n = 0.

Теперь выведем формулу (8), связывающую многочлены двух соседних степеней. Запишем (3):
(3)   y⁽ⁿ⁾ = p_n (x)( 1 – x² )^n – 12 = p_n ⋅ ( 1 – x² )^{–n + 12}.
Дифференцируем по x:
( ( 1 – x² )^{–n + 12} )^′ = ( –n + 12 )( 1 – x² )^{–n – 12} ( 1 – x² )^′ =
 –2n + 12 ( 1 – x² )^{–n – 12} ( –2x ) = (2n – 1) x( 1 – x² )^{–n – 12}; y^(n + 1) = p^′_n ⋅ ( 1 – x² )^{–n + 12} + p_n ⋅ ( ( 1 – x² )^{–n + 12} )^′ =
 p^′_n ⋅ ( 1 – x² )^{–n + 12} + (2n – 1) xp_n ⋅ ( 1 – x² )^{–n – 12} = (1 – x²) p^′_n + (2n – 1) xp_n( 1 – x² )^n + 12.
Поскольку   y^(n + 1) = p_n + 1 (x)( 1 – x² )^{n + 1 – 12},   то
(8)   p_n + 1 = (1 – x²) p^′_n + (2n – 1) xp_n.

Дифференциальное уравнение для многочленов

Теперь покажем, что многочлен p_n (x) удовлетворяет дифференциальному уравнению (10). Для этого мы используем формулы (8) и (9) и получим уравнение, содержащее только многочлен и его производные одной степени.

Дифференцируем (8) по x:
p^′_n + 1 = (1 – x²) p^′′_n + ( 1 – x² )^′ p^′_n + (2n – 1) xp^′_n + (2n – 1) (x)^′ p_n =
 (1 – x²) p^′′_n – 2xp^′_n + (2n – 1) xp^′_n + (2n – 1) p_n =
 (1 – x²) p^′′_n + (2n – 3) xp^′_n + (2n – 1) p_n;
(11)   p^′_n + 1 = (1 – x²) p^′′_n + (2n – 3) xp^′_n + (2n – 1) p_n.
Заменим в (8) n на n + 1:
p_n + 2 = (1 – x²) p^′_n + 1 + (2n + 1) xp_n + 1.
Подставим сюда (11) и (8):
p_n + 2 = (1 – x²) p^′_n + 1 + (2n + 1) xp_n + 1 =
 (1 – x²)[(1 – x²) p^′′_n + (2n – 3) xp^′_n + (2n – 1) p_n ] +
 (2n + 1) x ((1 – x²) p^′_n + (2n – 1) xp_n ) =
 (1 – x²)²  p^′′_n + [ 2n – 3 + 2n + 1 ] x(1 – x²)p^′_n + (2n – 1) [ (1 – x²) + (2n + 1)x² ]p_n =
 (1 – x²)²  p^′′_n + (4n – 2) x(1 – x²) p^′_n + (2n – 1)(1 + 2nx²) p_n.
Итак,
(12)   p_n + 2 = (1 – x²)²  p^′′_n + (4n – 2) x(1 – x²) p^′_n + (2n – 1)(1 + 2nx²) p_n.
Подставим (12) и (8) в (9):
(9)   p_n + 2 – (2n + 1) xp_n + 1 – n² (1 – x²) p_n = 0;
(1 – x²)²  p^′′_n + (4n – 2) x(1 – x²) p^′_n + (2n – 1)(1 + 2nx²) p_n –
 (2n + 1) x ((1 – x²) p^′_n + (2n – 1) xp_n ) – n² (1 – x²) p_n = 0;
(1 – x²)²  p^′′_n + (2n – 3) x(1 – x²) p^′_n + (2n – 1)(1 + 2nx²)p_n –
 (2n + 1)(2n – 1) x²  p_n – n² (1 – x²) p_n = 0.
Преобразуем коэффициент при p_n:
(2n – 1)(1 + 2nx²) – (2n + 1)(2n – 1) x² – n² (1 – x²) =
 (2n – 1)( 1 + 2nx² – (2n + 1) x² ) – n² (1 – x²) = (2n – 1)(1 – x²) – n² (1 – x²) =
  – (n² – 2n + 1)(1 – x²) =  – (n – 1)² (1 – x²).
Подставляем в предыдущее уравнение и сокращаем на (1 – x²):
(10)   (1 – x²) p^′′_n + (2n – 3) xp^′_n – (n – 1)²  p_n = 0.

Значения производных арксинуса высших порядков в нуле

Здесь мы покажем, что для нечетных n = 2m + 1, производная арксинуса в нуле, то есть при x = 0, имеет значение
(arcsin x)^(2m + 1) (0) = (1 ⋅ 3 ⋅ 5 ⋅ ...  ⋅ (2m – 1))² = ((2m – 1)!!)².
Для четных n = 2m, она равна нулю:
(arcsin x)^(2m) (0) = 0.

Поскольку
(arcsin x)⁽ⁿ⁾ = p_n (x)( 1 – x² )^n – 12,
то при x = 0,
(arcsin x)⁽ⁿ⁾ (0) = p_n (0)( 1 – 0² )^n – 12 = p_n (0).
То есть n-я производная арккосинуса в нуле равна значению многочлена p_n (x) в нуле. Таким образом, нам нужно найти значение многочлена при x = 0.

Выпишем уравнение (9) явно указывая, что p_n есть функция от x:
(9)   p_n + 2 (x) – (2n + 1) xp_n + 1 (x) – n² (1 – x²) p_n (x) = 0.
Подставим x = 0:
p_n + 2 (0) – n²  p_n (0) = 0, или
(13)   p_n + 2 (0) = n²  p_n (0).
Из этого уравнения легко получить значения многочленов p_n (x) в нуле.

Рассмотрим нечетные n. Для них n можно записать в виде:
n = 2m + 1,
где m = 0,  1,  2, ... – целое неотрицательное число. Воспользуемся формулой (3):
(3)   y⁽ⁿ⁾ = p_n (x)( 1 – x² )^n – 12.
Производная первого порядка нам известна:
(2)   y^′ = 1√ 1 – x² .
Отсюда p₁ (x) = 1. Это постоянная. Она имеет равные значения для всех x. Соответственно, при x = 0,
(14)   p₁ (0) = 1.

Подставим в (13) n = 1 и используем (14):
p₃ (0) = 1² ⋅ p₁ (0) = 1.
Аналогично, подставляем n = 3,  n = 5 и n = 7:
p₅ (0) = 3² ⋅ p₃ (0) = 3²;
p₇ (0) = 5² ⋅ p₅ (0) = 5² ⋅ 3²;
p₉ (0) = 7² ⋅ p₇ (0) = 7² ⋅ 5² ⋅ 3².
Теперь легко записать значение многочлена произвольной нечетной степени в нуле:
(15)   p_2m + 1 (0) = (1 ⋅ 3 ⋅ 5 ⋅ ...  ⋅ (2m – 1))² = ((2m – 1)!!)²;   p₁ (0) = 1.

Рассмотрим четные n. Выше мы нашли производную второго порядка:
y^′′ = x1 – x² y^′.
Отсюда p₂ (x) = x. Тогда p₂ (0) = 0. Используя формулу (13) получаем, что все четные производные в нуле равны нулю:
(16)   p_2m (0) = 0.

Вывод значений коэффициентов многочленов

Теперь мы можем найти значения коэффициентов многочленов. Запишем разложение многочлена по степеням x в общем виде:
(17)   p_n (x) = ^n – 1Σ_r = 0 a_r x^r.
Здесь a_r – коэффициенты, которые нам нужно найти.

Дифференцируя (17), находим первую и вторую производные:
(18)   p^′_n(x) = ^n – 1Σ_r = 0 ra_r x^r – 1.
p^′′_n(x) = ^n – 1Σ_r = 0 r(r – 1) a_r x^r – 2.
Подставляем их в (10) и выполняем преобразования:
(10)   (1 – x²) p^′′_n + (2n – 3) xp^′_n – (n – 1)²  p_n = 0;
(1 – x²)  ^n – 1Σ_r = 0 r(r – 1)a_r x^r – 2 + (2n – 3) x ^n – 1Σ_r = 0 ra_r x^r – 1 – (n – 1)^{2  n – 1}Σ_r = 0 a_r x^r = 0;
^n – 1Σ_r = 2 r(r – 1)a_r x^r – 2 – ^n – 1Σ_r = 0 r(r – 1)a_r x^r + (2n – 3)  ^n – 1Σ_r = 0 ra_r x^r – (n – 1)^{2  n – 1}Σ_r = 0 a_r x^r = 0.
Преобразуем три последних члена:
–r(r – 1) + (2n – 3)r – (n – 1)² = –r² + r + 2(n – 1)r – r – (n – 1)² =
 –r² + 2(n – 1)r – (n – 1)² =  – (n – r – 1)².
В первом члене заменим r → r + 2. Получаем:
^n – 3Σ_r = 0(r + 2)(r + 1)a_r + 2 x^r – ^n – 1Σ_r = 0(n – r – 1)²  a_r x^r = 0.
Отсюда получаем связь между коэффициентами при различных степенях x:
(19)   a_r + 2 = (n – r – 1)²(r + 1)(r + 2) a_r,   0 ≤ r ≤ n – 3.
Зная значения первых коэффициентов a₀ и a₁, по этой формуле можно определить значения остальных.

Нечетные n

Пусть n нечетно, n = 2m + 1.
Найдем значение первого коэффициента. В (15) мы нашли значение многочлена в нуле:
p_n (0) = ((n – 2)!!)² = ((2m – 1)!!)².
Но поскольку p_n (0) = a₀, то
a₀ = ((n – 2)!!)² = ((2m – 1)!!)².
Обозначим это значение буквой A:
A = (1 ⋅ 3 ⋅ 5 ⋅ ...  ⋅ (2m – 1))² = ((2m – 1)!!)²;
a₀ = A.

Найдем значение второго коэффициента. Для этого используем формулу производной многочлена:
(18)   p^′_n(x) = ^n – 1Σ_r = 0 ra_r x^r – 1.
Далее подставим сюда x = 0:
p^′_n(0) = a₁.
То есть значение второго коэффициента равно значению производной многочлена в нуле. Для ее нахождения, подставим в (8) значение x = 0:
p_n + 1 (0) = (1 – 0²) p^′_n(0) + (2n – 1) 0 ⋅ p_n (0).
Поскольку n нечетно, то n + 1 четно. Тогда из (16) следует, что p_n + 1 (0) = 0. Поэтому p^′_n(0) = 0. И вместе с этим
a₁ = 0.

Тогда из (19) следует, что поскольку a₁ = 0, то все коэффициенты нечетных степеней x равны нулю: a_2m + 1 = 0. Отличны от нуля только коэффициенты четных степеней, для которых r четно.

Подставим в (19) n = 2m + 1,  r = 2k – 2:
(19)   a_r + 2 = (n – r – 1)²(r + 1)(r + 2) a_r,   0 ≤ r ≤ n – 3.
n – r – 1 = 2m + 1 – 2k + 2 – 1 = 2m – 2k + 2 = 2(m – k + 1);
0 ≤ 2k – 2 ≤ 2m – 2;
2 ≤ 2k ≤ 2m;
(20)   a_2k = 2² (m – k + 1)²(2k – 1)(2k) a_2k – 2,   1 ≤ k ≤ m.

По формуле (20) найдем значения нескольких первых коэффициентов, учитывая, что коэффициент a₀ нам известен:
k = 1,  a₂ = 2² (m)²1 ⋅ 2 a₀;
k = 2,  a₄ = 2² (m – 1)²3 ⋅ 4 a₂ = 2⁴ (m)² (m – 1)²1 ⋅ 2 ⋅ 3 ⋅ 4 a₀;
k = 3,  a₆ = 2² (m – 2)²5 ⋅ 6 a₄ = 2⁶ (m(m – 1)(m – 2))²1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 a₀ = 2⁶ (m!)²((m – 3)!)² 6! a₀.

Отсюда не трудно установить общий вид коэффициентов:
a_2k = 2^2k (m!)²((m – k)!)² (2k)! a₀,   1 ≤ k ≤ m.
Тогда многочлен имеет вид:
p_2m + 1 (x) = a₀ + ^mΣ_k = 1 a_2k x^2k = A [1 + ^mΣ_k = 1 (m!)²(2k)!( (m – k)! )² (2x)^2k].

Четные n

Теперь рассмотрим четные n, n = 2m. Мы уже нашли, что для четных n, p_n (0) = 0. Поэтому
a₀ = 0.

Найдем значение второго коэффициента. Для этого подставим в (8) значение x = 0:
p_n + 1 (0) = (1 – 0²) p^′_n(0) + (2n – 1) 0 ⋅ p_n (0).
Отсюда
a₁ = p^′_n(0) = p_n + 1 (0) = ((n – 1)!!)² = ((2m – 1)!!)² = A.

Рассмотрим (19):
(19)   a_r + 2 = (n – r – 1)²(r + 1)(r + 2) a_r,   0 ≤ r ≤ n – 3.
Поскольку a₀ = 0, то все коэффициенты четных степеней x равны нулю: a_2m = 0. Отличны от нуля только коэффициенты нечетных степеней, для которых r нечетно. Тогда неравенства для r можно записать в виде:
1 ≤ r ≤ n – 3.

Подставим в (19) n = 2m,  r = 2k – 1:
n – r – 1 = 2m – 2k + 1 – 1 = 2(m – k);
1 ≤ 2k – 1 ≤ 2m – 3;
2 ≤ 2k ≤ 2m – 2;
(21)   a_2k + 1 = 2² (m – k)²(2k)(2k + 1) a_2k – 1,   1 ≤ k ≤ m – 1.

По этой формуле найдем значения нескольких первых коэффициентов:
k = 1,  a₃ = 2² (m – 1)²2 ⋅ 3 a₁;
k = 2,  a₅ = 2² (m – 2)²4 ⋅ 5 a₃ = 2⁴ (m – 1)² (m – 2)²1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 a₀;
k = 3,  a₇ = 2² (m – 3)²6 ⋅ 7 a₅ = 2⁶ ((m – 1)(m – 2)(m – 3))²1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 7 a₀ = 2⁶ ((m – 1)!)²((m – 4)!)² 7! a₀.

Устанавливаем общий вид коэффициентов:
a_2k + 1 = 2^2k ((m – 1)!)²((m – k – 1)!)² (2k + 1)! a₀,   1 ≤ k ≤ m – 1.
Тогда многочлен имеет вид:
p_2m (x) = a₁ x + ^m – 1Σ_k = 1 a_2k + 1 x^2k + 1 = x[ a₁ + ^m – 1Σ_k = 1 a_2k + 1 x^2k ] =
 Ax [1 + ^m – 1Σ_k = 1 ((m – 1!)²(2k + 1)!( (m – k – 1)! )² (2x)^2k].

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 01-06-2017