Производная суммы и разности функций

Приведена формула производной суммы и разности функций. Приведено доказательство и подробно разобраны примеры применения этой формулы.

Содержание

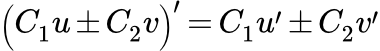
Формула производной суммы (разности) функций

Пусть функции u = u(x) и v = v(x) дифференцируемы в некоторой точке x. Тогда, в этой точке определена производная от суммы (разности) этих функций, и она равна сумме (разности) производных функций:
(1) (u ± v)^′ = u^′ ± v^′.

Доказательство

Поскольку функции u и v дифференцируемы в точке x, то существуют следующие пределы, которые являются производными этих функций:
u^′(x) = lim_{Δx → 0} u(x + Δx) – u(x)Δx;
v^′(x) = lim_{Δx → 0} v(x + Δx) – v(x)Δx.

Рассмотрим функцию y, которая является суммой функций u и v:
y(x) = u(x) + v(x).
Она определена в некоторой окрестности точки x. Покажем, что она имеет производную, и найдем ее.
y^′(x) = lim_{Δx → 0} y(x + Δx) – y(x)Δx = lim_{Δx → 0} u(x + Δx) + v(x + Δx) – u(x) – v(x)Δx=
lim_{Δx → 0}( u(x + Δx) – u(x)Δx + v(x + Δx) – v(x)Δx ) =
lim_{Δx → 0} u(x + Δx) – u(x)Δx + lim_{Δx → 0} v(x + Δx) – v(x)Δx = u^′(x) + v^′(x).

Тем самым мы доказали, что производная от суммы функций равна сумме производных:
(u + v)^′ = u^′ + v^′.

Тем же способом можно показать, что производная от разности функций равна разности производных:
(u – v)^′ = u^′ – v^′.
Это можно показать и другим способом, применяя только что доказанное правило дифференцирования суммы и правило вынесения постоянной за знак производной:
(u – v)^′ = (u + (–1) ⋅ v)^′ = u^′ + ((–1) ⋅ v)^′ = u^′ + (–1) ⋅ v^′ = u^′ – v^′.

Эти два правила можно записать в виде одного уравнения:
(1) (u ± v)^′ = u^′ ± v^′.

Следствие

Выше мы рассмотрели правило нахождения производной от суммы двух функций. Это правило можно обобщить на сумму и разность от любого числа дифференцируемых функций.

Производная от суммы (разности) любого конечного числа дифференцируемых функций равна сумме (разности) их производных. С учетом правила вынесения постоянной за знак производной, это правило можно записать так:
( ⁿΣ_i = 1 C_i u_i )^′ = ⁿΣ_i = 1 C_i u^′_i.
Или в развернутом виде:
(2) (C₁ u₁ + C₂ u₂+... +C_n u_n )^′ = C₁ u^′₁ + C₂ u^′₂ +... +C_n u^′_n.
Здесь C₁, C₂, ..., C_n – постоянные;
u₁, u₂, ..., u_n – дифференцируемые функции от переменной x.

Доказательство следствия

При n = 2, применим правило (1) и правило вынесения постоянной за знак производной. Имеем:
( C₁ u₁ + C₂ u₂ )^′ = (C₁ u₁)^′ + (C₂ u₂)^′ = C₁ u^′₁ + C₂ u^′₂.
При n = 3 применим формулу (1) для функций u = C₁ u₁ + C₂ u₂ и v = C₃ u₃:
( C₁ u₁ + C₂ u₂ + C₃ u₃ )^′ = ( C₁ u₁ + C₂ u₂ )^′ + (C₃ u₃)^′ = C₁ u^′₁ + C₂ u^′₂ + C₃ u^′₃.

Для произвольного числа n применим метод индукции. Пусть уравнение (2) выполняется для n = m. Тода для n = m + 1 имеем:
( ^m + 1Σ_i = 1 C_i u_i )^′ = ( ^mΣ_i = 1 C_i u_i + C_m + 1 u_m + 1 )^′ = ( ^mΣ_i = 1 C_i u_i )^′ + (C_m + 1 u_m + 1)^′ =
^mΣ_i = 1 C_i u^′_i + C_m + 1 u^′_m + 1 = ^m + 1Σ_i = 1 C_i u^′_i.
То есть из предположения, что уравнение (2) выполняется для n = m следует, что уравнение (2) выполняется для n = m + 1. А поскольку уравнение (2) выполняется для n = 2, то оно выполняется для всех n.
Следствие доказано.

Примеры

Все примеры Далее мы приводим примеры вычислений производных суммы и разности с подробными решениями.
y(x) = x³ (x² – 1)² ⇓, y(x) = √ x + ln x – 1√ x ⇓, y(x) = √ 2x – 5 ³√ x + 3x² ⇓.

Пример 1

Все примеры ⇑ Найдите производную
y(x) = x³ (x² – 1)².

Решение

Раскрываем скобки. Для этого применим формулу
(a – b)² = a² – 2ab + b².
Также используем свойства степенных функций.
(x² – 1)² = ( x² )² – 2x² + 1 = x^2 ⋅ 2 – 2x² + 1 = x⁴ – 2x² + 1;
x³ (x² – 1)² = x³ (x⁴ – 2x² + 1) = x³ x⁴ – 2x³ x² + x³ =
x^3 + 4 – 2x^3 + 2 + x³ = x⁷ – 2x⁵ + x³;
y(x) = x⁷ – 2x⁵ + x³.

Применяем формулу (2) для производной от суммы и разности функций.
y^′(x) = (x⁷ – 2x⁵ + x³)^′ = (x⁷)^′ – 2(x⁵)^′ + (x³)^′.

Из таблицы производных находим:
(x^a)^′ = ax^a – 1.
Тогда
(x⁷)^′ = 7x^7 – 1 = 7x⁶;
(x⁵)^′ = 5x^5 – 1 = 5x⁴;
(x³)^′ = 3x^3 – 1 = 3x².

Окончательно имеем:
y^′(x) = (x⁷)^′ – 2(x⁵)^′ + (x³)^′ = 7x⁶ – 2 ⋅ 5x⁴ + 3x² = 7x⁶ – 10x⁴ + 3x².

Ответ

y^′(x) = 7x⁶ – 10x⁴ + 3x².

Пример 2

Все примеры ⇑ Найти производную от функции от переменной x
y(x) = √ x + ln x – 1√ x .

Решение

Приведем корни к степенным функциям.
y(x) = x^1 / 2 + ln x – x^–1 / 2.
Применяем правило дифференцирования суммы и разности.
y^′(x) = ( x^1 / 2 + ln x – x^–1 / 2 )^′ = ( x^1 / 2 )^′ + (ln x)^′ – ( x^–1 / 2 )^′.
Применяем формулы из таблицы производных.
(ln x)^′ = 1x;
(x^a)^′ = ax^a – 1;
( x^1 / 2 )^′ = 12 x^12 – 1 = 12 x^– 12;
12 – 1 = 12 – 22 = – 12;
( x^–1 / 2 )^′ = – 12 x^{– 12 – 1} = – 12 x^– 32;
– 12 – 1 = – 12 – 22 = – 32.
Подставляем:
y^′(x) = ( x^1 / 2 )^′ + (ln x)^′ – ( x^–1 / 2 )^′ = 12 x^– 12 + 1x + 12 x^– 32 = 12 √ x + 1x + 12 √ x³ .
Приводим дроби к общему знаменателю.
√ x³ = √ x² x = | x | √ x = x √ x .
Здесь мы учли, что заданная функция определена при x > 0.
y^′(x) = 12 √ x + 1x + 12x √ x = x + 2 √ x + 12x √ x .

Ответ

y^′(x) = x + 2 √ x + 12x √ x .

Пример 3

Все примеры ⇑ Найти производную функции
y(x) = √ 2x – 5 ³√ x + 3x².

Решение

Преобразуем функцию. Для этого применим свойства степенной функции и корней:
y(x) = √ 2x – 5 ³√ x + 3x² = √ 2x x² – 5 ³√ x x² + 3x² = (2x)^1 / 2x² – 5 x^1 / 3x² + 3x^–2 =
2^1 / 2 x^1 / 2x² – 5x^13 – 2 + 3x^–2 = √ 2 x^12 – 2 – 5x^{13 – 63} + 3x^–2 = √ 2 x^–3 / 2 – 5 x^–5 / 3 + 3 x^–2;
12 – 2 = 12 – 42 = – 32;
13 – 2 = 13 – 63 = – 53;
y(x) = √ 2 x^–3 / 2 – 5 x^–5 / 3 + 3 x^–2.

Находим производную, применяя правило (2):
y^′(x) = ( √ 2 x^–3 / 2 – 5 x^–5 / 3 + 3 x^–2 )^′ = √ 2 ( x^–3 / 2 )^′ – 5( x^–5 / 3 )^′ + 3( x^–2 )^′ =
√ 2 ⋅ ( – 32 ) x^{– 32 – 1} – 5 ⋅ ( – 53 )x^{– 53 – 1} + 3 ⋅ (–2) x^{–2 – 1} =
– 3√ 2 x^– 52 + 253 x^– 83 – 6 x^–3 = – 3√ 2 √ x⁵ + 253 ³√ x⁸ – 6x³.

Здесь мы применили формулу из таблицы производных:
( x^a )^′ = a x^a – 1

Ответ

y^′ = – 3√ 2 x⁵ + 253 ³√ x⁸ – 6x³

Автор: Олег Одинцов. Опубликовано: 18-10-2016 Изменено: 13-11-2023