Примеры как найти производные второго и высших порядков
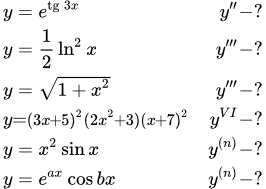
Применяемые правила и методы
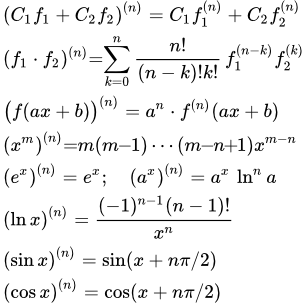
Чтобы найти производные высших порядков произвольной функции, нужно применить одно или несколько следующих правил и теорем: теорему производной суммы функций, произведения (формула Лейбница), формулы производных высших порядков элементарных функций. Эти правила изложены на странице
Производные второго и высших порядков – основные формулы, определения и теоремы
Кроме этого применяют некоторые приемы, позволяющие упростить вычисления. Это преобразование к неявной функции и использование комплексных чисел.
Преобразование к неявной функции применяют, чтобы дифференцировать более простое выражение. Вот несколько примеров.
При нахождении производных от , можно избавиться от корня, если возвести это равенство в квадрат: , и далее находить производные от более простой неявной зависимости (пример 3).
Функцию удобно прологарифмировать: (пример 1).
Дробь можно умножить на знаменатель: , и дифференцировать произведение, а не частное (пример 2).
Использование комплексных чисел может быть полезным при дифференцировании некоторых функций, в состав которых входит синус и косинус. Суть метода заключается в том, что вместо исходной функции вводят комплексную:
.
Дифференцируя n раз, получим:
.
Отсюда n-я производная исходной функции равна действительной части производной n-го порядка комплексной функции :
.
Например, . Дифференцируя n раз имеем:
.
Учитывая, что ,
получаем известные формулы производных синуса и косинуса:
;
.
Примеры с решениями
Все примеры Здесь мы рассмотрим следующие примеры вычислений производных высших порядков.
Найти y′, y′′ от функции y′′′ – ?
y′′′ – ?
yVI – ?
Найти n-ю производную,
Пример 1
Все примеры Найти производные первого и второго порядка следующей функции:
(П1.1) .
Решение преобразованием к неявной функции
Можно последовательно дифференцировать заданную функцию. Этот способ рассмотрен ниже. Но мы сделаем преобразование, чтобы находить производные от более простых выражений. Логарифмируя (П1.1), получаем неявную зависимость от :
(П1.1.1) .
Дифференцируем по переменной :
(П1.1.2) .
Находим производные в (П1.1.2), вводя переменную , и применяя правило дифференцирования составной функции.
;
;
;
.
Подставляем в (П1.1.2):
(П1.1.3) .
Используя (П1.1), получаем первую производную:
;
(П1.1.4) .
Чтобы проще находить вторую производную, преобразуем уравнение (П1.1.3), умножив его на , и дифференцируем по :
;
(П1.1.5) .
Находим производную левой части, применяя правила дифференцирования произведения и сложной функции, вводя переменные .
;
;
;
.
Подставляем в (П1.1.5), и используем (П1.1.4):
;
;
.
Ответ
;
.
Решение стандартным способом
Находим производную первого порядка. Выносим постоянную за знак производной и применяем формулу из таблицы производных:
.
Применяем правило дифференцирования сложной функции:
.
Здесь .
Применяем правило дифференцирования сложной функции и используем найденные производные:
.
Здесь .
Итак, мы нашли производную первого порядка:
.
Чтобы найти производную второго порядка, нам нужно найти производную от первой производной, то есть от функции
.
Чтобы не путаться с обозначениями, обозначим эту функцию буквой :
(П1.2.1) .
Тогда производная второго порядка от исходной функции является производной от :
.
Дифференцируем . Это проще сделать с помощью логарифмической производной. Логарифмируем (П1.2.1):
.
Теперь дифференцируем:
(П1.2.2) .
Но – это постоянная. Ее производная равна нулю. Производную от мы уже нашли. Находим оставшуюся производную по правилу дифференцирования сложной функции, вводя переменные .
;
;
.
Подставляем в (П1.2.2):
.
Отсюда
.
Ответ
;
.
Пример 2
Все примеры Найти производную третьего порядка:
.
Решение
Находим производную первого порядка. Для этого выносим постоянную за знак производной, используем таблицу производных и применяем правило нахождения производной сложной функции.
.
Здесь .
Итак, мы нашли производную первого порядка:
(П2.1) .
Находим производную второго порядка. Для этого находим производную от . Применяем формулу производной дроби.
.
Производная второго порядка:
.
Теперь находим искомую производную третьего порядка. Для этого дифференцируем .
;
;
.
Можно сделать по другому, избавившись от дробей. Умножим (П2.1) на :
(П2.2) .
Дифференцируем.
;
.
Снова умножаем на , и находим производную.
(П2.3) ;
;
.
.
Умножаем на и применяем (П2.2) и (П2.3)
.
Отсюда
.
Ответ
Производная третьего порядка равна
.
Пример 3
Все примеры Найти производную третьего порядка от функции
(П3.1) .
Решение
Чтобы избавиться от корня, возводим (П3.1) в квадрат.
.
Дифференцируем три раза, попутно выполняя преобразования.
;
;
(П3.2) ;
;
;
(П3.3) ;
;
;
.
Умножим на , и применим (П3.2) и (П3.3).
;
.
Ответ
Производная третьего порядка равна
.
Пример 4
Все примеры Найти производную шестого порядка следующей функции:
.
Решение
Если раскрыть скобки, то будет ясно, что исходная функция является многочленом степени . Запишем ее в виде многочлена:
,
где – постоянные коэффициенты.
Далее применим формулу n-й производной степенной функции:
.
Для производной шестого порядка (n = 6) имеем:
.
Отсюда видно, что при . При имеем:
.
Используем формулу производной суммы функций:
.
Таким образом, чтобы найти производную шестого порядка исходной функции, нам надо найти только коэффициент многочлена при старшей степени . Находим его, перемножая старшие степени в произведениях сумм исходной функции:
.
Отсюда . Тогда
.
Ответ
.
Пример 5
Все примеры Найти n-ю производную функции
.
Пример 6
Все примеры Найти n-ю производную следующей функции:
,
где и – постоянные.
Решение
В этом примере вычисления удобно выполнять с использованием комплексных чисел. Пусть мы имеем некоторую комплексную функцию
,
где и – функции от действительной переменной x;
– мнимая единица, .
Дифференцируя n раз, имеем:
.
Иногда проще найти n-ю производную от функции . Тогда n-е производные функций и определяются как действительная и мнимая части от n-й производной :
;
.
Применим этот прием для решения нашего примера. Рассмотрим функцию
.
Здесь мы применили формулу Эйлера
,
и ввели обозначение
.
Тогда n-я производная исходной функции определяется по формуле:
.
Найдем n-ю производную функции
.
Для этого применим формулу:
.
В нашем случае
.
Тогда
.
Итак, мы нашли n-ю производную комплексной функции :
,
где .
Найдем действительную часть функции .
Для этого представим комплексное число в показательной форме:
,
где ;
; .
Тогда
;
.
Решение примера
.
Пусть , .
Тогда ;
.
При ,
,
,
.
И мы получаем формулу n-й производной косинуса:
.
Ответ
,
где
; .
Автор: Олег Одинцов. Опубликовано: Изменено:
