Доказательство второго замечательного предела и его следствий
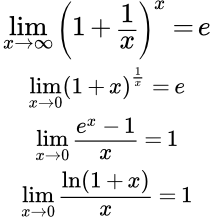
Второй замечательный предел и его следствия
Второй замечательный предел – это предел, на основе которого вычисляются производные показательной функции и логарифма.
Лемма. Второй замечательный предел
.
Здесь x – действительное число.
Доказательство ⇓
Следствия второго замечательного предела
1) ;
2) ; ;
3) ; ;
4) ; ; ; .
Доказательство ⇓
Доказательство второго замечательного предела
При доказательстве мы будем использовать тот факт, что последовательность строго возрастает и имеет конечный предел, равный числу e: .
Доказательство приведено на странице «Число e – его смысл и доказательство сходимости последовательности».
Сначала рассмотрим правый предел
.
Для его существования должна существовать такая окрестность точки , на которой функция определена. В нашем случае, определена при . Но мы можем выбрать любую окрестность. Для удобства считаем, что .
Пусть – функция, которая означает, целую часть числа x. Например: . Она не убывает. Рассмотрим сложную функцию
.
Докажем, что она имеет предел при , равный числу e: .
Поскольку последовательность строго возрастает, а функция не убывает, то сложная функция не убывает. Тогда по теореме о пределе монотонной функции, имеет конечный или бесконечный предел при :
.
Покажем, что . Для этого используем определение предела функции по Гейне, согласно которому, если функция имеет предел при : , то для любой последовательности , сходящейся к , последовательность сходится к A: . Возьмем последовательность . Она сходится к . Тогда . Но последовательность совпадает с :
.
Поэтому ее предел равен . Таким образом A = e:
(1) .
Сделаем подстановку . Заметим, что . Заменив переменную t на x получим:
(2) .
Теперь воспользуемся тем, что . Тогда
;
(3) .
Далее замечаем, что
, .
Применяем арифметические свойства предела функции и пределы (1) и (2):
;
.
Применяя к (3) теорему о промежуточной функции, получаем, что
.
Теперь рассмотрим левый предел
.
Считаем, что . Сделаем подстановку . Тогда . При .
.
Применяем арифметические свойства предела функции.
.
Поскольку существуют равные пределы справа и слева, то существует и двусторонний предел
.
Второй замечательный предел доказан.
Доказательство следствий второго замечательного предела
1) Докажем, что .
Делаем замену переменной . Тогда . При . Поэтому
.
Заметим, что фактически мы представили как сложную функцию , где . Далее мы применили теорему о пределе сложной функции.
Следствие 1) доказано.
2) Докажем, что .
Выполняем преобразования, учитывая что показательная функция является обратной к логарифмической:
.
Делаем замену переменной . В силу непрерывности показательной функции,
. Поскольку при , то
.
В предпоследнем равенстве мы воспользовались непрерывностью логарифмической функции и теоремой о пределе непрерывной функции от функции. В последнем равенстве мы применили следствие второго замечательного предела.
Также заметим, что применяя подстановку, мы представили функцию как сложную:
, где , и применили теорему о пределе сложной функции.
Применяем арифметические свойства предела функции:
.
Также здесь мы воспользовались свойством логарифма: .
Полагая a = e, имеем:
.
Следствие 2) доказано.
3) Докажем, что .
Выполняем преобразования.
.
Функция определена при . Логарифм непрерывен на своей области определения. Применяем доказанное выше следствие 1 и теорему о пределе непрерывной функции от функции:
.
Также здесь мы воспользовались свойством логарифма: .
Подставляя a = e, получаем:
.
4) Докажем, что .
Для этого воспользуемся определением гиперболического синуса и следствием 2) ⇑. Выполняем преобразования.
.
Докажем, что .
Для этого используем определения гиперболических функций и предыдущий предел.
;
.
Докажем, что .
Для этого сделаем замену переменной .
Тогда при ; при ;
(см. «Обратные гиперболические функции, их графики и формулы»).
.
Докажем, что .
Сделаем замену переменной .
Тогда при ; при ;
при (см. «Обратные гиперболические функции, их графики и формулы»).
.
Следствия доказаны.
Автор: Олег Одинцов. Опубликовано: Изменено:
