Примеры пределов с решениями

Страница содержит ссылки на 45 примеров решений пределов функций и 24 задачи на смежные темы. К смежным темам относятся задачи на применение определений предела последовательности и предела функции, а также задачи на непрерывность функции.

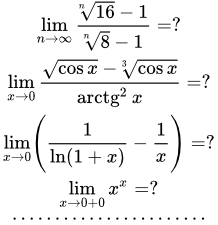
• Попробуйте решить указанные ниже задачи на вычисление пределов и смежные вопросы.
• Нажмите на изображение или стрелку, чтобы попасть на страницу с подробным решением.

Определение предела последовательности

Используя определение предела последовательности доказать, что
  >>>         >>>         >>>         >>>         >>>

Применяя теорему о промежуточной последовательности, и используя то, что , найти пределы:
  >>>         >>>

Используя определение бесконечно большой последовательности доказать, что
  >>>         >>>         >>>         >>>

Пользуясь теоремой Вейерштрасса, доказать сходимость последовательности:
,   ,   . . . ,   , . . . ,
после чего найти ее предел.
Решение >>>

Определение предела функции

Используя определение предела функции по Коши (эпсилон и дельта рассуждения) доказать, что
  >>>         >>>         >>>         >>>         >>>         >>>

Непрерывность функции

Используя определения по Гейне и Коши доказать, что функция непрерывна для всех x.   Решение >>>
Используя определение непрерывности по Коши доказать, что функция непрерывна для всех .   Решение >>>

Задана функция и два значения аргумента и . Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа, установить вид разрыва; 3) сделать схематический чертеж.
.   Решение >>>

Задана функция . Найти точки разрыва функции, если они существуют. Указать род разрыва и скачек функции, если есть. Сделать чертеж.
.   Решение >>>

Определить точки разрыва функции и исследовать характер этих точек, если
.   Решение >>>

Докажите, что уравнение , где n – натуральное, – действительное неотрицательное число, имеет единственное решение на множестве действительных чисел, . Это решение называется корнем степени n из числа a. То есть нужно показать, что любое неотрицательное число имеет единственный корень степени n.   Решение >>>

Вычисление пределов

Найти, если существует, предел функции:
.   Решение >>>

Найти односторонние пределы сложной функции в точке :
  и  .   Решение >>>

Найти предел функции или последовательности.
  >>>         >>>         >>>         >>>         >>>         >>>         >>>         >>>         >>>         >>>       >>>         >>>         >>>         >>>         >>>         >>>       >>>         >>>         >>>         >>>         >>>         >>>         >>>         >>>         >>>         >>>         >>>         >>>

Вычислить предел последовательности, используя разложение в ряд Тейлора.
  >>>
Вычислить пределы, используя разложение функций в ряд Тейлора.
  >>>         >>>         >>>       >>>

Найти пределы, используя правило Лопиталя.
  >>>         >>>         >>>         >>>         >>>         >>>

Найти пределы, применяя эквивалентные функции.
  >>>         >>>         >>>         >>>

Автор: Олег Одинцов.     Опубликовано: 16-05-2019   Изменено: 09-02-2020