Интегрирование рациональной функции от квадратного корня из квадратного трехчлена

Представлен наиболее эффективный способ интегрирования рациональной функции от квадратного корня из квадратного трехчлена. Разобран пример вычисления такого интеграла.

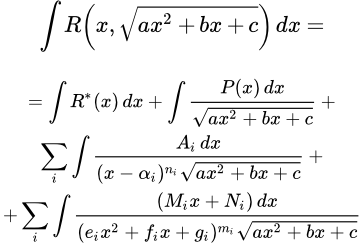
Метод интегрирования

Здесь мы рассматриваем интегралы вида:
,
где R – рациональная функция.

Ранее мы рассмотрели интегралы с квадратным корнем от трехчлена трех типов.
(i)     Подробнее >>>
(ii)     Подробнее >>>
(iii)     Подробнее >>>
Здесь P_n (x) – многочлен степени n от x.

Покажем, что любой интеграл от рациональной функции вида , можно выразить через интегралы (i), (ii) и (iii) и интеграл от рациональной функции   .

Доказательство

Прежде всего заметим, что любая целая степень от квадратного корня     является или многочленом (для четных степеней), или произведением многочлена на корень   .
Действительно, имеем.
;
;
;
;
И так далее.

Любую рациональную функцию можно представить в виде дроби, в числителе и знаменателе которой стоят суммы конечного числа членов от целочисленных степеней ее аргументов.
.
Поскольку целая степень от квадратного корня является или многочленом от x, или произведением многочлена на корень, то
,
где P(x), Q(x), V(x), W(x) – многочлены от x.

Умножим числитель и знаменатель на     и применим формулу (a + b)(a – b) = a ² – b ².
В знаменателе имеем.


.
Как видно, знаменатель становится многочленом, который мы обозначили через U(x). В числителе по прежнему имеется сумма произведений целочисленных степеней от x и   . Поэтому числитель имеет прежний вид , где P^*(x), Q^*(x) - многочлены. Таким образом, имеем
,
где R(x) – рациональная функция, Q^**(x) – многочлен.

Если степень многочлена Q^**(x) больше, чем у многочлена U(x), то выделим целую часть. Тогда
,
где P^**(x) – многочлен, – правильная дробь. Имеем . Правильную дробь     разложим на простейшие. Это даст сумму членов вида     и   .

Подставляя все члены разложения в     и интегрируя получаем, что интеграл     выражается через интегралы вида   ,   ,     и   .

Что и требовалось доказать.

Пример

Найти интеграл

Решение

Умножим числитель и знаменатель на   .

.

Интегрируем.

Ищем решение оставшегося интеграла в виде
.
Дифференцируем по x.



.
Умножая на    , имеем
.
Сравнивая левую и правую части, находим значения коэффициентов.
2A = 1,    A = 1/2;
B = 0;
D – A = – 1,   D = A – 1 = – 1/2.

Окончательно имеем.
;
.

Ответ

.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 16-02-2015