Вычисление неопределенных интегралов от многочленов

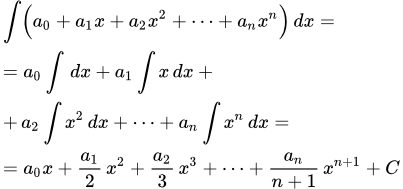
Формула интеграла от многочлена в общем виде. Примеры вычисления интегралов от многочленов и степенных функций, применяя основные методы интегрирования.

Формула интеграла от многочлена

Представим, для справок, формулу интеграла от многочлена в общем виде. Пусть задан многочлен от переменной x степени n
,
где a₀, a₁, a₂, ... , a_n – постоянные, не зависящие от x коэффициенты.

Неопределенный интеграл от многочлена определяется по формуле

,
где C – постоянная интегрирования.

Интегрирование многочленов

Рассмотрим процесс интегрирования многочленов более подробно.

Интегрирование многочленов – это самый простой вид интегрирования. Он основан на двух правилах.
1)   Правило интегрирования суммы или разности.

2)   Вынесение постоянной за знак интеграла.
,
где u, v, w – функции от переменной интегрирования x;
c – постоянная, не зависящая от x.

Также мы применяем один табличный интеграл
.

Далее рассмотрим интегрирование многочленов на примерах.

Примеры

Далее рассмотрены примеры вычислений следующих интегралов.
     

Примеры вычисления неопределенных интегралов от многочленов

Пример 1

Найти неопределенный интеграл от многочлена
.

Решение

Замечаем, что подынтегральное выражение     является суммой и разностью трех членов:
x⁴,   3x² и 5x.
Применяем правило 1.

Замечаем, что подынтегральные функции двух последних интегралов умножены на постоянные 3 и 5, соответственно. Применяем правило 2.
(1.1)  

Теперь применим формулу из таблицы интегралов
.
Подставим в нее n = 4:
.
Подставим n = 2:
.
Подставим n = 1:
.

Подставляем найденные интегралы в (1.1).

И, наконец, прибавим постоянную интегрирования.

Ответ

Пример 2

Найти неопределенный интеграл от многочлена во второй степени
.

Решение

Подынтегральная функция является квадратом от многочлена. Чтобы вычислить неопределенный интеграл, нужно возвести многочлен в квадрат. Для этого мы используем формулу

и воспользуемся свойством степенной функции:

.

Также, можно было бы перемножить сомножители:

.

В результате мы получаем интеграл от многочлена
.

Здесь подынтегральное выражение     является суммой и разностью трех членов:
x⁴,   2x² и 1.
Применяем правило 1.

Подынтегральная функция второго интеграла умножена на постоянную 2. Применяем правило 2.

Интеграл от единицы, можно записать, как и во всех формулах, опустив множитель 1:
.

Тогда
(2.1)   .

Теперь применим формулу из таблицы интегралов
.
Подставим в нее n = 4:
.
Подставим n = 2:
.
Подставим n = 0:
.

Подставляем найденные интегралы в (2.1).

Прибавим постоянную интегрирования в ответ.

Ответ

Похожие примеры вычисления неопределенных интегралов от степеней

Здесь мы применяем формулы и свойства степенных функций.

Пример 3

Найти неопределенный интеграл
.

Решение

Преобразуем подынтегральную функцию.
(x + 1)² = x² + 2x + 1;
;
;
.

Интегрируем, применяя формулу из таблицы интегралов
.

.
;
;
.

.

Ответ

Пример 4

Найти неопределенный интеграл
.

Решение

Преобразуем подынтегральную функцию, используя свойства степенной функции.
;
;
;
.

Интегрируем, применяя формулу из таблицы интегралов
.
;
;
.

Ответ

.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 19-09-2015