Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции

Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых содержит логарифм, арксинус, арктангенс, а также логарифм в целой степени и логарифм от многочлена.

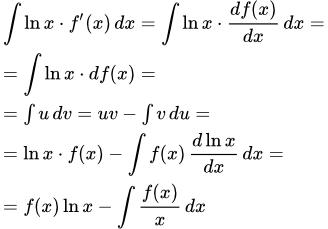
Формула интегрирования по частям

Ниже, при решении примеров, применяется формула интегрирования по частям:
;
.
Подробнее >>>

Примеры интегралов, содержащих логарифм и обратные тригонометрические функции

Вот примеры интегралов, которые интегрируются по частям:
      ,      

При интегрировании ту часть подынтегрального выражения, которая содержит логарифм или обратные тригонометрические функции обозначают через u, остальное – через dv.

Ниже приведены примеры с подробными решениями этих интегралов.

Простой пример с логарифмом

Вычислим интеграл, содержащий произведение многочлена и логарифма:

Решение

Здесь подынтегральное выражение содержит логарифм. Делаем подстановки
u = ln x, dv = x² dx. Тогда
,
.

Интегрируем по частям.
.

Вычисляем оставшийся интеграл:
.
Тогда
.
В конце вычислений добавим постоянную C.

Ответ

Пример логарифма в степени 2

Рассмотрим пример, в котором в подынтегральное выражение входит логарифм в целочисленной степени. Такие интегралы также могут интегрироваться по частям.

Решение

Делаем подстановки
u = (ln x)², dv = x dx. Тогда
,
.

.

Оставшийся интеграл также вычисляем по частям:
.
Подставляем
.

Ответ

Пример, в котором аргумент логарифма является многочленом

По частям могут вычисляться интегралы, в подынтегральное выражение которого входит логарифм, аргумент которого является многочленом, рациональной или иррациональной функцией. В качестве примера, вычислим интеграл с логарифмом, аргумент которого является многочленом.
.

Решение

Делаем подстановки
u = ln( x² – 1), dv = x dx.
Тогда
,
.

.

Вычисляем оставшийся интеграл:
.
Мы здесь не пишем знак модуля ln |x² – 1|, поскольку подынтегральное выражение определено при x² – 1 > 0. Подставляем
.

Ответ

Пример с арксинусом

Рассмотрим пример интеграла, в подынтегральное выражение которого входит арксинус.
.

Решение

Делаем подстановки
u = arcsin x,
.
Тогда
,
.

.

Далее замечаем, что подынтегральное выражение определено при |x| < 1. Раскроем знак модуля под логарифмом, учитывая что 1 – x > 0 и 1 + x > 0.

Ответ

Пример с арктангенсом

Решим пример с арктангенсом:
.

Решение

Интегрируем по частям.
.
Выделим целую часть дроби:
x⁸ = x⁸ + x⁶ – x⁶ – x⁴ + x⁴ + x² – x² – 1 + 1 = (x² + 1)(x⁶ – x⁴ + x² – 1) + 1;
.
Интегрируем:
.
Окончательно имеем:
.

Ответ

Еще один пример с арксинусом

Решить интеграл:
.

Решение

Интегрируем по частям.
.

Вычисляем оставшийся интеграл. При x > 0 имеем:
.
.
.

При x < 0 сделаем подстановку x = – t,   t > 0:
.

Окончательно имеем:

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 19-10-2014