Основные формулы и методы интегрирования

Основные формулы и методы интегрирования. Правило интегрирования суммы или разности. Вынесение постоянной за знак интеграла. Метод замены переменной. Формула интегрирования по частям. Пример решения задачи.

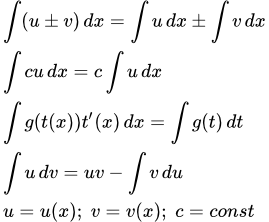
Методы интегрирования

Ниже перечислены четыре основных метода интегрирования.

1)   Правило интегрирования суммы или разности.
∫ (u ± v ± w )dx = ∫ u dx ± ∫ v dx ± ∫ w dx .
Здесь и далее u, v, w – функции от переменной интегрирования x .

2)   Вынесение постоянной за знак интеграла.
Пусть c – постоянная, не зависящая от x . Тогда ее можно вынести за знак интеграла. ∫ cu dx = c ∫ u dx

См. подробнее: Вычисление интегралов от многочленов >>>

3)   Метод замены переменной.
Рассмотрим неопределенный интеграл   ∫  f (x ) dx .
Если удастся подобрать такую функцию φ(x) от x , так что
 f (x ) = g( φ(x ) ) φ^′(x ) ,
то, выполнив замену переменной t = φ(x) , имеем
∫  f (x ) dx = ∫ g( φ(x ) ) φ^′(x ) dx = ∫ g(t ) dt .

См. подробнее: Интегрирование методом замены переменной >>>

4)   Формула интегрирования по частям.
∫ u dv = uv – ∫ v du ,
где u и v – это функции от переменной интегрирования.

См. подробнее: Метод интегрирования неопределенного интеграла по частям >>>

Конечная цель вычисления неопределенных интегралов – это, путем преобразований, привести заданный интеграл к простейшим интегралам, которые называются табличными. Табличные интегралы выражаются через элементарные функции по известным формулам.
См. Таблица интегралов >>>

Пример

Вычислить неопределенный интеграл
I = ∫ ( 5x²  – 4x ln x + 2x² ln x  ) dx

Решение

Замечаем, что подынтегральная функция  f (x ) = 5x²  – 4x ln x + 2x² ln x является суммой и разностью трех членов:
5x² ,   4x ln x   и   2x² ln x .
Применяем метод 1.
I = ∫ 5x²  dx – ∫ 4x ln x  dx + ∫ 2x² ln x dx =
 ∫ 5x²  dx – ∫ 4 ⋅ 1x ln x  dx + ∫ 2x² ln x dx

Далее замечаем, что подынтегральные функции новых интегралов умножены на постоянные 5, 4, и 2 , соответственно. Применяем метод 2.
I = 5 ∫ x²  dx – 4 ∫ dxx ln x + 2 ∫ x² ln x dx

В таблице интегралов находим формулу
∫ xⁿ  dx = 1n + 1 x^n + 1 .
Полагая n = 2 , находим первый интеграл.
I₁  = ∫ x²  dx = 12 + 1 x^2 + 1  = 13 x³

Перепишем второй интеграл в виде
I₂  = ∫ dxx ln x = ∫ 1ln x ⋅ 1x ⋅ dx .
Замечаем, что   (ln x )^′ = 1x . Тогда
I₂  = ∫ 1ln x ⋅ (ln x )^′ dx
Применяем третий метод. Делаем замену переменной   t = φ(x) = ln x .
I₂  = ∫ 1ln x ⋅ (ln x )^′ dx ≡ ∫ 1ln x ⋅ d(ln x )dx  dx = ∫ 1ln x  d(ln x ) = ∫ 1t  dt ≡ ∫ dtt .
В таблице интегралов находим формулу
∫ dxx = ln  | x | 
Поскольку переменная интегрирования может обозначаться любой буквой, то
I₂  = ∫ dtt = ln  | t |  = ln  |  ln x | 

Перепишем третий интеграл в виде
I₃  = ∫ x² ln x dx = ∫ ln x ⋅ x²  dx .
Применяем формулу интегрирования по частям.
Положим   u = ln x,  dv = x²  dx .
Тогда
du = dudx dx ≡ u^′ dx = (ln x )^′ dx = dxx ;
v = ∫ dv = ∫ x²  dx = 12 + 1 x^2 + 1  = 13 x³ ;
I₃  = ∫ ln x ⋅ x²  dx = ∫ u dv = uv – ∫ v du = ln x ⋅ 13 x³  – ∫ 13 x³ dxx =
 13 x³ ln x – 13 ∫ x²  dx ;
∫ x²  dx = 13 x³ ;
I₃  = 13 x³ ln x – 19 x³ .

Окончательно имеем
I = 5I₁  – 4I₂  + 2I₃  = 53 x³  – 4 ln  |  ln x |  + 23 x³ ln x – 29 x³ .
Соберем члены с   x³ .
53 x³  – 29 x³  = 159 x³  – 29 x³  = 139 x³ .

Ответ

I = 139 x³  – 4 ln  |  ln x |  + 23 x³ ln x + C

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 10-09-2015