Вычисление интегралов от многочлена дробь степень от двучлена квадратный корень из квадратного трехчлена

Представлен метод вычисления интегралов, в числителе дроби которых находится многочлен, а в знаменателе – произведение натуральной степени от линейной функции и квадратный корень из квадратного трехчлена. Разобраны примеры вычислений таких интегралов.

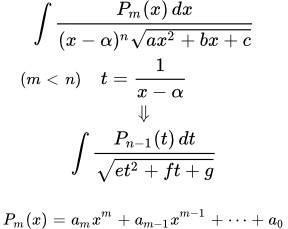
Метод интегрирования

Рассмотрим интеграл от дроби, в числителе которой стоит многочлен степени m, а в знаменателе - целая положительная степень от линейной функции и квадратный корень из квадратного трехчлена:
∫ P_m (x ) dx(x – α )ⁿ √ ax²  + bx + c  .
Здесь n - натуральное число.

Если m ≥ n , то у дроби   P_m (x )(x – α )ⁿ   следует выделить целую часть, после чего интеграл разбивается на два интеграла. Один – без степенной функции в знаменателе:
∫ P_m – n (x ) dx√ ax²  + bx + c 
Второй – исходного типа с правильной дробью:
∫ P_n – 1 (x ) dx(x – α )ⁿ √ ax²  + bx + c  ,

Подстановкой   t = (x – α)^–1 этот интеграл приводится к интегралу вида:
∫ Q_n – 1 (t ) dt√ et²  +  ft + g  .
Здесь Q_n–1 – многочлен, степени не выше n – 1 . Таким образом, вычисление исходных интегралов сводится к вычислению интегралов вида
∫ Q(t ) dt√ et²  +  ft + g  .
Метод интегрирования таких интегралов разобран на странице
Вычисление интегралов от многочлена дробь квадратный корень из квадратного трехчлена > > >.

Важное замечание

При вычислении подобных интегралов, после подстановки, приходится извлекать квадратный корень из квадрата: √ t²  . При этом нужно иметь в виду, что √ t²  =  | t |  . То есть, при t > 0, |t| = t , при t < 0, |t| = – t . Поэтому при вычислении подобных интегралов, нужно отдельно рассматривать случаи t > 0 и t < 0 . Это можно сделать, если писать знаки ± или ∓ там, где это необходимо. Подразумевая, что верхний знак относится к случаю t > 0 , а нижний - к случаю t < 0 . При обратном преобразовании к переменной x , эти знаки, как правило, взаимно сокращаются.

Также возможен второй подход, в котором мы не следим за знаком подкоренного выражения, а получаем многозначную комплексную функцию. Более подробно см здесь > > >.

Полезная формула

Отметим полезную формулу, которую стоит помнить, выполняя преобразования:
ln | τ – √ τ²  ± σ²   | = – ln | τ + √ τ²  ± σ²   | + ln σ²
В частности, при σ = 1 ,
ln | τ – √ τ²  ± 1   | = – ln | τ + √ τ²  ± 1   |

Для доказательства, применим формулу:
(a – b)(a + b) = a ² – b ²
Положим a = τ , b = √ τ²  ± σ²  ,  b²  = τ²  ± σ² .
( τ – √ τ²  ± σ²   )( τ + √ τ²  ± σ²   ) = ∓ σ²
Приравняем модули и логарифмируем:
| τ – √ τ²  ± σ²   | ⋅ | τ + √ τ²  ± σ²   | = σ² ;
ln | τ – √ τ²  ± σ²   | + ln | τ + √ τ²  ± σ²   | = ln σ² ;
Отсюда
ln | τ – √ τ²  ± σ²   | = – ln | τ + √ τ²  ± σ²   | + ln σ²

Примеры

Здесь рассмотрим два простых примера
I = ∫ dxx √ 1 – a² x²    I = ∫ dxx √ x²  – 1    , демонстрирующих извлечение квадратного корня из квадрата, и влияние этой операции на конечный результат. В конце решим более сложный интеграл I = ∫ x dx(x – 1 )² √ x²  + 1 

Пример 1

Вычислим интеграл
I = ∫ dxx √ 1 – a² x² 

I = ∫ dxx √ 1 – a² x²  = ∫ dxx √ x² (x^– 2  – a² )  = ∫ dxx | x | √ (x^– 2  – a² )  =
± ∫ dxx² √ (x^– 2  – a² )  = ± ∫ x^– 2  dx√ x^– 2  – a²  = ∓ ∫d( x^– 1  )√ (( x^– 1  )²  – a² )  =
∓ ln | x^– 1  + √ x^– 2  – a²   | = ∓ ln | 1x + √ 1 – a² x²x²   | = ∓ ln | 1x + √ 1 – a² x²  | x |   | =
∓ ln | 1x ± √ 1 – a² x² x  |
Здесь верхний знак соответствует значениям x > 0 . Нижний – значениям x < 0 .

Таким образом, при x > 0
I = – ln | 1x + √ 1 – a² x² x  | + C
При x < 0
I = ln | 1x – √ 1 – a² x² x  | + C = – ln | 1x + √ 1 – a² x² x  | + ln a²  + C ;

Постоянную ln a ² включим в C . В результате получаем выражение для интеграла в виде одной формулы, справедливой как для x > 0 , так и для x < 0 :
I = – ln | 1x + √ 1 – a² x² x  | + C = – ln 1 + √ 1 – a² x²  | x |  + C

Пример 2

Вычислим интеграл
I = ∫ dxx √ x²  – 1 

I = ∫ dxx √ x²  – 1  = ∫ dxx √ x² (1 – x^– 2 )  = ∫ dxx | x | √ (1 – x^– 2 )  =
± ∫ dxx² √ (1 – x^– 2 )  = ± ∫ x^– 2  dx√ 1 – x^– 2  = ∓ ∫ d( x^– 1  )√ (1 – ( x^– 1  )² )  =
∓ arcsin (x^– 1 ) = ∓ arcsin 1x = – arcsin ( ± 1x  ) = – arcsin ( 1± x  ) = – arcsin 1 | x | 
Здесь верхний знак соответствует значениям x > 0 . Нижний - значениям x < 0 .

Таким образом, если, для рассматриваемых интегралов, ответ выражается через арксинусы, то появляется знак модуля.

Более сложный пример

Вычислить интеграл:
I = ∫ x dx(x – 1 )² √ x²  + 1 

Решение

Здесь дробь x(x – 1 )² правильная, поэтому выделять целую часть не нужно.

Делаем подстановку t = (x – 1) ^-1 . Для этого выполняем преобразования.
x²  + 1 = x²  – 2x + 1 + 2x – 2 + 2 = (x – 1 )²  + 2(x – 1 ) + 2 ;
(x – 1 )² ( 1 + 2(x – 1 )^– 1  +    2(x – 1 )^– 2  ) = (x – 1 )²  s²
Здесь s = √ 1 + 2(x – 1 )^– 1  + 2(x – 1 )^– 2  = √ 2t²  + 2t + 1  .
Извлекаем корень.
√ x²  + 1  = √ (x – 1 )²  s²  =  | x – 1 |  s = ± (x – 1 ) s
Далее будем считать, что верхний знак соответствует значениям x – 1 > 0 или, что тоже что, t > 0 . Нижний знак - значениям x – 1 < 0 (t < 0).
dt = ( (x – 1 )^– 1  )^′ dx = – (x – 1 )^– 2  dx = – dx(x – 1 )²

Подставляем.
± I = ∫ x dx(x – 1 )³  s = ∫ x – 1 + 1x – 1 ⋅ dxs(x – 1 )² = ∫ ( 1 + (x – 1 )^– 1  ) dxs (x – 1 )² =
– ∫ (1 + t ) dts = – ∫ (1 + t ) dt√ 2t²  + 2t + 1 
Решаем методом неопределенных коэффициентов. Ищем решение в виде:
± I = – ∫ (1 + t ) dts = A s + B ∫ dts
Дифференцируем по t .
s^′ = ( ( 2t²  + 2t + 1  )^1 / 2  )^′ = 12 ( 2t²  + 2t + 1  )^{– 1 / 2}  ⋅ ( 2t²  + 2t + 1  )^′ =
4t + 22s = 2t + 1s ;
– ( ∫ (1 + t ) dts  )^′ = As^′ + B( ∫ dts  )^′ ;
– (1 + t )s = A 2t + 1s + Bs ;
– t – 1 = A(2t + 1 ) + B = 2At + A + B ;
2A = – 1 , A = – 1/2 , A + B = – 1 , B = – 1 – A = – 1/2 .

Итак, мы нашли:
± I = – 12 √ 2t²  + 2t + 1  – 12 ∫ dt√ 2t²  + 2t + 1  = – 12 s – 12 I₂ .

Вычисляем оставшийся интеграл.
s²  = 2t²  + 2t + 1 = 2( t²  + t + 12  ) = 2( t²  + 2 ⋅ t ⋅ 12 + 14 + 14  ) = 2( ( t + 12  )²  + ( 12  )²  ) ;
√ ( t + 12  )²  + ( 12  )²  = s√ 2  ;
I₂  = ∫ dt√ 2t²  + 2t + 1  = 1√ 2  ∫d( t + 12  )√ ( t + 12  )²  + ( 12  )²  =
1√ 2  ln |  t + 12 + √ ( t + 12  )²  + ( 12  )²  | + C =
± 1√ 2  ln |  t + 12 ± √ ( t + 12  )²  + ( 12  )²  | + C = ± 1√ 2  ln |  t + 12 ± s√ 2   | + C .
Здесь мы постоянную   ln ( 12  )²   включили в C .

Переходим к переменной x , используя полученную ранее формулу:   s = ± √ x²  + 1 x – 1 .
I₂  = ± 1√ 2  ln  | 1x – 1 + 12 + √ x²  + 1 √ 2  (x – 1 )  | + C =
± 1√ 2  ln ( 12  | 2x – 1 + 1 +    2 √ x²  + 1 √ 2  (x – 1 )  |  ) + C =
± 1√ 2  ln ( 12  | 2 + x – 1x – 1 +    √ 2(x²  + 1 ) x – 1  |  ) + C =
± 1√ 2  ln ( 12  ) ± 1√ 2  ln |  x + 1 + √ 2x²  + 2 x – 1  | + C =
± 1√ 2  ln |  x + 1 + √ 2x²  + 2 x – 1  | + C .
Здесь мы постоянную   ± 1√ 2  ln ( 12  )   включили в C .

Окончательно имеем:
± I = – 12 s – 12 I₂  = ∓ √ x²  + 1 2(x – 1 ) ∓ 12 √ 2  ln |  x + 1 + √ 2x²  + 2 x – 1  | + C .

Ответ

I = – √ x²  + 1 2(x – 1 ) – 12 √ 2  ln |  x + 1 + √ 2x²  + 2 x – 1  | + C

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 15-01-2015   Изменено: 03-01-2016