Примеры интегрирования рациональных функций (дробей)
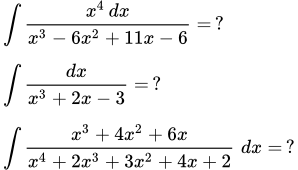
Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей:
, , .
Пример 1
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя (3) меньше степени многочлена числителя (4). Поэтому, вначале необходимо выделить целую часть дроби.
1. Выделим целую часть дроби. Делим x 4 на x 3 – 6x 2 + 11x – 6:
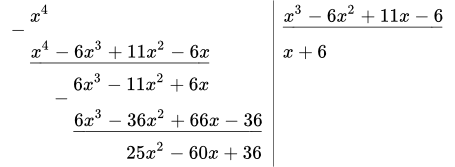
Отсюда
.
2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, 3, 6, –1, –2, –3, –6.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим на x – 1:
Отсюда
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.
3. Разложим дробь на простейшие.
.
Итак, мы нашли:
.
Интегрируем.
Ответ
.
Пример 2
Вычислить интеграл:
.
Решение
Здесь в числителе дроби – многочлен нулевой степени (1 = x 0). В знаменателе – многочлен третьей степени. Поскольку 0 < 3, то дробь правильная. Разложим ее на простейшие дроби.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x). То есть целый корень может быть одним из чисел:
1, 3, –1, –3.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим x 3 + 2x – 3 на x – 1:
Итак,
.
Решаем квадратное уравнение:
x 2 + x + 3 = 0.
Находим дискриминант: D = 1 2 – 4·3 = –11. Поскольку D < 0, то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x – 1)(x 2 + x + 3):
(2.1) .
Подставим x = 1. Тогда x – 1 = 0,
.
Подставим в (2.1) x = 0:
1 = 3A – C;
.
Приравняем в (2.1) коэффициенты при x 2:
;
0 = A + B;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.
;
;
.
Вычисляем I2.
.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0. Поэтому знак модуля можно опустить.
Поставляем в (2.2):
.
Ответ
.
Пример 3
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит дробь из многочленов. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли один корень x = –1. Делим на x – (–1) = x + 1:
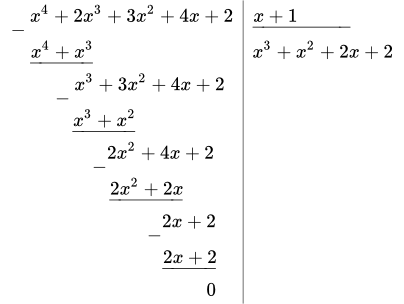
Итак,
.
Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли еще один корень x = –1. Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.
Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x + 1) 2(x 2 + 2):
(3.1) .
Подставим x = –1. Тогда x + 1 = 0,
.
Продифференцируем (3.1):
;
.
Подставим x = –1 и учтем, что x + 1 = 0:
;
; .
Подставим в (3.1) x = 0:
0 = 2A + 2B + D;
.
Приравняем в (3.1) коэффициенты при x 3:
;
1 = B + C;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
