Интегрирование произведения многочлена, экспоненты и синуса или косинуса
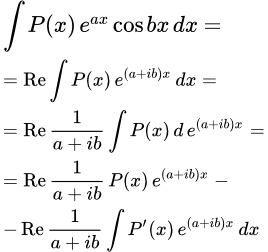
Метод интегрирования с помощью формулы Эйлера
Рассмотрим интегралы вида:
, ,
где P(x) – многочлен от x.
Здесь подынтегральное выражение линейно относительно одной из функций
cos ax или sin ax, Поэтому удобно применить формулу Эйлера:
eiax = cos ax + isin ax (где i2 = –1 – мнимая единица)
и вычислять интеграл
.
Тогда по формуле Эйлера имеем:
.
После вычисления интеграла I0, отделяя его действительную и мнимые части, получаем искомые интегралы:
I1 = Re I0, I2 = Im I0.
Метод интегрирования без комплексных чисел
Для вычисления таких интегралов, можно было бы обойтись без комплексных чисел, однако вычисления были бы более громоздкими.
Для этого нам пришлось бы интегрировать по частям, полагая u = P(x), dv = cos ax ebx.
Далее нужно было бы найти v, вычисляя интеграл . Для вычисления этого, промежуточного интеграла, пришлось бы два раза проинтегрировать по частям и получить формулу приведения, из которой и определить v.
Затем, интегрируя по частям, мы получили бы аналогичные интегралы, многочлен которых имел бы степень, на единицу меньше, чем у исходного. Далее следовало бы повторять этот процесс до тех пор, пока степень многочлена станет равной нулю.
Пример
Вычислить интеграл:
Решение
Применим формулу Эйлера:
eix = cos x + isin x
Для этого рассмотрим интеграл:
.
После вычисления I0, искомый интеграл определим по формуле:
I = Im I0.
Обозначим p = 1 + i, тогда
.
Интегрируем по частям, используя соотношение между дифференциалами.
.
.
Оставшийся интеграл также интегрируем по частям:
.
Окончательно имеем:
.
Приводим комплексные числа к алгебраической форме.
;
.
Умножаем числитель и знаменатель на выражение, комплексно сопряженное знаменателю.
;
;
.
Подставляем в I0
Мнимая часть дает искомый интеграл.
Ответ
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
