Интегрирование рациональных функций (дробей)

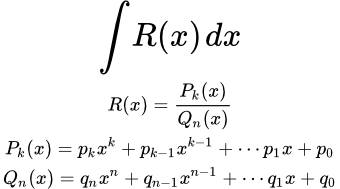
Стандартный метод интегрирования рациональных функций: выделение целой части дроби многочленов, разложение правильной дроби на простейшие, интегрирование простейших дробей. Нестандартные методы интегрирования рациональных функций: применение степенных и дробно-линейных подстановок, интегралы с возвратными многочленами.

Стандартные методы интегрирования рациональных функций

Рациональная функция R(x) от переменной x – это функция, образованная, из переменной x и произвольного конечного количества постоянных, с помощью конечного числа операций сложения, вычитания, умножения и деления. Алгебраическими преобразованиями ее можно привести к дроби из двух многочленов от переменной x:
,
где ,
– многочлены степеней k и n, соответственно.

Рассмотрим интеграл от рациональной функции:
(1)  
Далее приводится стандартный метод вычисления таких интегралов.

1. Если k ≥ n, то мы делим многочлен P_k(x) на многочлен Q_n(x). В результате получаем:
(2)   ,
где – многочлен степени k–n;
– многочлен степени m < n.

См. подробнее: Деление и умножение многочлена на многочлен уголком и столбиком >>>

2. Раскладываем многочлен Q_n(x) на множители:

См. подробнее: Методы разложения многочленов на множители >>>
Примеры разложения многочленов на множители >>>

3. Раскладываем правильную рациональную дробь на простейшие:

См. подробнее: Методы разложения рациональных дробей на простейшие >>>

4. Подставляем в (2) и интегрируем. В результате исходный интеграл (1) выражается через более простые интегралы следующих видов:
;
;
.

5. Вычисляем интегралы от простейших дробей.
См. подробнее: Интегрирование простейших дробей >>>
Примеры интегрирования рациональных функций >>>

Нестандартные методы интегрирования рациональных функций

Иногда удается найти подстановку, которая приводит к более простым интегралам. Ниже рассмотрены подобные случаи.

Применение простых степенных подстановок

В некоторых случаях удается найти степенную подстановку вида t = xⁿ, которая приводит интеграл к более простому виду.

Пример

Вычислить интеграл:

Решение

Умножим числитель и знаменатель на x⁷:
.

Делаем подстановку t = x⁸:
.

Разложим дробь на простейшие.
.

Интегрируем:
.
Поскольку x⁸ ≥ 0, то знак модуля можно убрать. По свойству модуля и логарифма:
.

Ответ

.

Дробно-линейные подстановки

Интегралы вида легко находятся с помощью дробно-линейной подстановки   , применяя формулы:
;
;
.

Пример

Вычислить интеграл:
.

Решение

Преобразуем знаменатель.
x² – 1 = (x – 1)(x + 1);
;
.

Делаем дробно-линейную подстановку:
.
;
;
;
;

.

Применяем формулу бинома Ньютона:
.
;
.

Интегрируем.
.

Ответ

;
.

Возвратные многочлены

Некоторые интегралы, содержащие возвратные многочлены и множитель x² – 1 или x² + 1, находятся подстановкой     или   . Вот примеры таких интегралов:
, , , .

Пример

Вычислить интеграл
.

Решение

Введем вспомогательные интегралы:
,
,
.

Разделим числитель и знаменатель на x² и делаем подстановку   .

.

Разделим числитель и знаменатель на x² и делаем подстановку   .

.
Поскольку уравнения

корней не имеют, то   . Поэтому знак модуля можно опустить.

Искомый интеграл
.

Ответ

.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 24-08-2015