Примеры разложения многочленов на множители

Приводится 8 примеров разложения многочленов на множители. Они включают в себя примеры с решением квадратных и биквадратных уравнений, примеры с возвратными многочленами и примеры с нахождением целых корней у многочленов третьей и четвертой степени.

Здесь рассмотрены следующие примеры разложения многочленов на множители:
             
См. также Примеры решений неопределенных интегралов

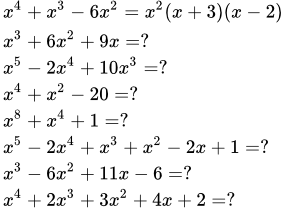
Примеры с решением квадратного уравнения

Пример 1.1

Разложить многочлен на множители:
.

Решение

Выносим x² за скобки:
.
Решаем квадратное уравнение x² + x – 6 = 0:
.
Корни уравнения:
,   .

Отсюда получаем разложение многочлена на множители:
.

Ответ

.

Пример 1.2

Разложить на множители многочлен третьей степени:
.

Решение

Выносим x за скобки:
.
Решаем квадратное уравнение x² + 6x + 9 = 0:
Его дискриминант:   .
Поскольку дискриминант равен нулю, то корни уравнения кратные: ;
.

Отсюда получаем разложение многочлена на множители:
.

Ответ

.

Пример 1.3

Разложить на множители многочлен пятой степени:
.

Решение

Выносим x³ за скобки:
.
Решаем квадратное уравнение x² – 2x + 10 = 0.
Его дискриминант:   .
Поскольку дискриминант меньше нуля, то корни уравнения комплексные: ;
,   .

Разложение многочлена на множители имеет вид:
.

Если нас интересует разложение на множители с действительными коэффициентами, то:
.

Ответ

.

Примеры с биквадратными многочленами

Пример 2.1

Разложить биквадратный многочлен на множители:
.

Решение

Применим формулы:
a² + 2ab + b² = (a + b)²;
a² – b² = (a – b)(a + b).

;
.

Ответ

.

Пример 2.2

Разложить на множители многочлен, сводящийся к биквадратному:
.

Решение

Применим формулы:
a² + 2ab + b² = (a + b)²;
a² – b² = (a – b)(a + b):

;

;
.

Ответ

.

Пример с возвратным многочленом

Разложить на множители возвратный многочлен:
.

Решение

Возвратный многочлен имеет нечетную степень. Поэтому он имеет корень x = –1. Делим многочлен на x – (–1) = x + 1. В результате получаем:
.
Делаем подстановку:
,   ;
;


;
.

Ответ

.

Примеры разложения многочленов на множители с целыми корнями

Пример 3.1

Разложить многочлен на множители:
.

Решение

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
–6, –3, –2, –1, 1, 2, 3, 6.
Подставляем поочередно эти значения:
(–6)³ – 6·(–6)² + 11·(–6) – 6 = –504;
(–3)³ – 6·(–3)² + 11·(–3) – 6 = –120;
(–2)³ – 6·(–2)² + 11·(–2) – 6 = –60;
(–1)³ – 6·(–1)² + 11·(–1) – 6 = –24;
1³ – 6·1² + 11·1 – 6 = 0;
2³ – 6·2² + 11·2 – 6 = 0;
3³ – 6·3² + 11·3 – 6 = 0;
6³ – 6·6² + 11·6 – 6 = 60.

Итак, мы нашли три корня:
x₁ = 1, x₂ = 2, x₃ = 3.
Поскольку исходный многочлен – третьей степени, то он имеет не более трех корней. Поскольку мы нашли три корня, то они простые. Тогда
.

Ответ

.

Пример 3.2

Разложить многочлен на множители:
.

Решение

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
–2, –1, 1, 2.
Подставляем поочередно эти значения:
(–2)⁴ + 2·(–2)³ + 3·(–2)³ + 4·(–2) + 2 = 6;
(–1)⁴ + 2·(–1)³ + 3·(–1)³ + 4·(–1) + 2 = 0;
1⁴ + 2·1³ + 3·1³ + 4·1 + 2 = 12;
2⁴ + 2·2³ + 3·2³ + 4·2 + 2 = 54.

Итак, мы нашли один корень:
x₁ = –1.
Делим многочлен на x – x₁ = x – (–1) = x + 1:

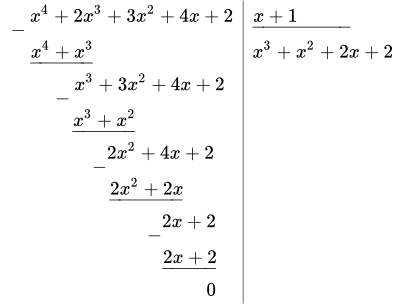
Тогда,
.

Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.

Итак, мы нашли еще один корень x₂ = –1. Можно было бы, как и в предыдущем случае, разделить многочлен     на   , но мы сгруппируем члены:
.

Поскольку уравнение x ² + 2 = 0 не имеет действительных корней, то разложение многочлена на множители имеет вид:
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 18-06-2015