Методы разложения многочленов на множители

Доказано, что для разложения многочлена на множители, нужно найти его корни. Формулы корней квадратного многочлена. Метод нахождения целых корней. Метод разложения на множители биквадратного многочлена и приводящихся к квадратным. Возвратные многочлены.

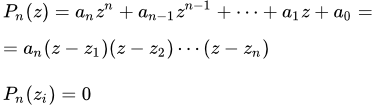
Основа метода

Пусть

– многочлен степени n ≥ 1 от действительной или комплексной переменной z с действительными или комплексными коэффициентами a_i. Примем без доказательства следующую теорему.

Теорема 1

Докажем следующую лемму.

Лемма 1

Доказательство

Разложение многочлена на множители

Итак, на основании теоремы 1, многочлен P_n(z) имеет хотя бы один корень. Обозначим его как z₁, P_n(z₁ ) = 0. Тогда на основании леммы 1:
P_n(z) = (z – z₁)P_n–1(z).
Далее, если n > 1, то многочлен P_n–1(z) также имеет хотя бы один корень, который обозначим как z₂, P_n–1(z₂ ) = 0. Тогда
P_n–1(z) = (z – z₂)P_n–2(z);
P_n(z) = (z – z₁)(z – z₂)P_n–2(z).

Продолжая этот процесс, мы приходим к выводу, что существует n чисел z₁, z₂, ... , z_n таких, что
P_n(z) = (z – z₁)(z – z₂) ... (z – z_n)P₀(z).
Но P₀(z) – это постоянная. Приравнивая коэффициенты при z ⁿ, находим что она равна a_n. В результате получаем формулу разложения многочлена на множители:
(1)   P_n(z) = a_n(z – z₁)(z – z₂) ... (z – z_n).

Числа z_i являются корнями многочлена P_n(z).

В общем случае не все z_i, входящие в (1), различны. Среди них могут оказаться одинаковые значения. Тогда разложение многочлена на множители (1) можно записать в виде:
(2)   P_n(z) = a_n(z – z₁) ^n₁ (z – z₂)^n₂ ... (z – z_k)^n_k ;
.
Здесь z_i ≠ z_j при i ≠ j. Если n_i = 1, то корень z_i называется простым. Он входит в разложение на множители в виде (z–z_i). Если n_i > 1, то корень z_i называется кратным корнем кратности n_i. Он входит в разложение на множители в виде произведения n_i простых множителей: (z–z_i)(z–z_i) ... (z–z_i) = (z–z_i)^n_i.

Многочлены с действительными коэффициентами

Далее мы считаем, что многочлен

имеет действительные коэффициенты a_i.

Лемма 2

Доказательство

Таким образом, комплексные корни входят в разложение на множителями парами со своими комплексно сопряженными значениями:
,
где ,   – действительные числа.
Тогда разложение (2) многочлена с действительными коэффициентами на множители можно представить в виде, в котором присутствуют только действительные постоянные:
(3)   ;
.

Методы разложения многочлена на множители

С учетом сказанного выше, для разложения многочлена на множители, нужно найти все корни уравнения P_n(z) = 0 и определить их кратность. Множители с комплексными корнями нужно сгруппировать с комплексно сопряженными. Тогда разложение определяется по формуле (3).

Таким образом, метод разложения многочлена на множители заключается в следующем:
1.   Находим корень z₁ уравнения P_n(z₁) = 0.
2.1.   Если корень z₁ действительный, то в разложение добавляем множитель (z – z₁) и делим многочлен P_n(z) на (z – z₁). В результате получаем многочлен степени n – 1:
.
Далее повторяем процесс для многочлена P_n–1(z), начиная с пункта 1, пока не найдем все корни.
2.2.   Если корень    комплексный, то и комплексно сопряженное число является корнем многочлена. Тогда в разложение входит множитель

,
где b₁ = – 2 x₁, c₁ = x₁² + y₁².
В этом случае, в разложение добавляем множитель (z ² + b₁z + c₁) и делим многочлен P_n(z) на (z ² + b₁z + c₁). В результате получаем многочлен степени n – 2:
.
Далее повторяем процесс для многочлена P_n–2(z), начиная с пункта 1, пока не найдем все корни.

Нахождение корней многочлена

Главной задачей, при разложении многочлена на множители, является нахождение его корней. К сожалению, не всегда это можно сделать аналитически. Здесь мы разберем несколько случаев, когда можно найти корни многочлена аналитически.

Корни многочлена первой степени

Многочлен первой степени – это линейная функция. Она имеет один корень. Разложение имеет только один множитель, содержащий переменную z :
.

Корни многочлена второй степени

Чтобы найти корни многочлена второй степени, нужно решить квадратное уравнение:
P₂(z) = a₂z ² + a₁z + a₀ = 0.
Если дискриминант   , то уравнение имеет два действительных корня:
,   .
Тогда разложение на множители имеет вид:
.
Если дискриминант D = 0, то уравнение имеет один двукратный корень:
;
.
Если дискриминант D < 0, то корни уравнения комплексные,
.

Многочлены степени выше второй

Существуют формулы для нахождения корней многочленов 3-ей и 4-ой степеней. Однако ими редко пользуются, поскольку они громоздкие. Формул для нахождения корней многочленов степени выше 4-ой нет. Несмотря на это, в некоторых случаях, удается разложить многочлен на множители.

Нахождение целых корней

Если известно, что многочлен, у которого коэффициенты – целые числа, имеет целый корень, то его можно найти, перебрав все возможные значения.

Лемма 3

Пусть многочлен
,
коэффициенты a_i которого – целые числа, имеет целый корень z₁. Тогда этот корень является делителем числа a₀.

Доказательство

Поэтому, если коэффициенты многочлена – целые числа, то можно попытаться найти целые корни. Для этого нужно найти все делители свободного члена a₀ и, подстановкой в уравнение P_n(z) = 0, проверить, являются ли они корнями этого уравнения.
Примечание. Если коэффициенты многочлена – рациональные числа,   , то умножая уравнение P_n(z) = 0 на общий знаменатель чисел a_i, получим уравнение для многочлена с целыми коэффициентами.

Нахождение рациональных корней

Если коэффициенты многочлена – целые числа и целых корней нет, то при a_n ≠ 1, можно попытаться найти рациональные корни. Для этого нужно сделать подстановку
z = y/a_n
и умножить уравнение на a_n^n-1. В результате мы получим уравнение для многочлена от переменной y с целыми коэффициентами.Далее ищем целые корни этого многочлена среди делителей свободного члена. Если мы нашли такой корень y_i , то перейдя к переменной x, получаем рациональный корень
z_i = y_i  /a_n.

Полезные формулы

Приведем формулы, с помощью которых можно разложить многочлен на множители.

В более общем случае, чтобы разложить многочлен
P_n(z) = zⁿ – a₀,
где a₀ – комплексное, нужно найти все его корни, то есть решить уравнение:
zⁿ = a₀.
Это уравнение легко решается, если выразить a₀ через модуль r и аргумент φ:
.
Поскольку a₀ не изменится, если к аргументу прибавить 2π, то представим a₀ в виде:
,
где k – целое. Тогда
;
.
Присваивая k значения k = 0, 1, 2, ... n–1, получаем n корней многочлена. Тогда его разложение на множители имеет вид:
.

Биквадратный многочлен

Рассмотрим биквадратный многочлен:
.
Биквадратный многочлен можно разложить на множители, без нахождения корней.

При   , имеем:

,
где   .

При   , имеем:

,
где   .

Далее раскладываем квадратные многочлены на множители, если соответствующие многочлены имеют действительные корни.

Бикубический и многочлены, приводящиеся к квадратному

Рассмотрим многочлен:
.
Его корни определяются из уравнения:
.
Оно приводится к квадратному уравнению подстановкой t = zⁿ:
a_2n t² + a_n t + a₀ = 0.
Решив это уравнение, найдем его корни, t₁, t₂. После чего находим разложение в виде:
.
Далее методом, указанным выше, раскладываем на множители zⁿ – t₁ и zⁿ – t₂. В заключении группируем множители, содержащие комплексно сопряженные корни.

Возвратные многочлены

Многочлен     называется возвратным, если его коэффициенты симметричны:

Пример возвратного многочлена:
.

Если степень возвратного многочлена n – нечетна, то такой многочлен имеет корень z = –1. Разделив такой многочлен на z + 1, получим возвратный многочлен степени n – 1.
Если степень возвратного многочлена n – четна, то подстановкой   , он приводится к многочлену степени n/2. См. Пример с возвратным многочленом >>>.

См. далее Примеры разложения многочленов на множители > > >

Автор: Олег Одинцов.     Опубликовано: 11-06-2015   Изменено: 30-04-2016