Интегрирование дифференциального бинома

Интегралы от дифференциального бинома сводятся к интегралам от рациональных функций в трех случаях, при определенных соотношениях между показателями степеней. Даны три подстановки, которые приводят к интегралу от рациональной функции. Даны формулы приведения, связывающие интегралы с различными значениями показателей степеней. Подробно разобран пример вычисления интеграла от дифференциального бинома.

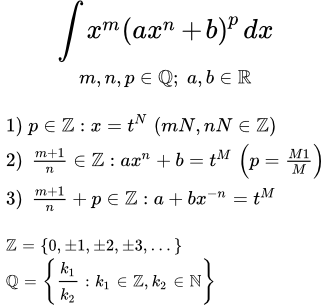
Применяемые подстановки

Рассмотрим интеграл:
,
где m, n, p – рациональные числа, a, b – действительные числа.
Подынтегральное выражение называется дифференциальным биномом. Интеграл от него сводится к интегралам от рациональных функций в трех случаях.

  1)   Если p – целое, то выполняется подстановка x = t ^N, где N – общий знаменатель дробей m и n.
  2)   Если – целое, то подстановка a x ⁿ + b = t ^M, где M – знаменатель числа p.
  3)   Если – целое, подстановка a + b x ^{– n} = t ^M, где M – знаменатель числа p.

Если ни одно из трех чисел     не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.

Формулы приведения (понижения или повышения показателей степеней)

В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям показателей степеней m и p. Это можно сделать с помощью формул приведения:
;
.

Доказательство формул приведения

Доказательство первой формулы

Докажем первую формулу:

Выполняем преобразования.


Интегрируем по частям, умножив на na(p+1).
u = x^m–n+1, v = (axⁿ + b) ^p+1, du = (x^m–n+1)′ dx = (m–n+1) x^m–n dx.

Преобразуем оставшийся интеграл.

Подставляем.

Отсюда

Или
.

Доказательство второй формулы

Докажем вторую формулу:
.

Выполняем преобразования.


Интегрируем по частям, умножив на m + 1.
u = (axⁿ + b)^p, v = x^m+1,

Преобразуем оставшийся интеграл.

Подставляем.

Отсюда
.

Пример

Вычислить интеграл.

Решение

Преобразуем.

Это интеграл от дифференциального бинома

со значениями m = 1/3, p = 1/3, n = 2, a = – 1, b = 1.
Поскольку
– целое, то интеграл сводится к интегралу от рациональной функции третьей подстановкой:
– 1 + x ^{– 2} = t ³.

Возьмем дифференциал от обеих частей этого равенства.


Подставляем

Интегрируем по частям.

Разложим дробь на простейшие.

Выделим в числителе второй дроби производную знаменателя и преобразуем знаменатель.
(t² – t + 1)′ = 2t – 1

Подставляем

Интегрируем

Окончательно имеем

Ответ

где .

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 05-12-2014