Обратные функции – определение и свойства

Определение обратной функции и ее свойства: теорема о взаимной монотонности прямой и обратной функций; симметрия графиков прямой и обратной функций; теоремы о существовании и непрерывности обратной функции для функции, строго монотонной на отрезке, интервале и полуинтервале. Примеры обратных функций. Пример решения задачи.

Содержание

См. также:

Определение и свойства

Обратная функция: Пусть функция имеет область определения X и множество значений Y. И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X, для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.

Из определения следует, что
;
для всех ;
для всех .

Теорема о существовании и монотонности обратной функции

Если функция f строго возрастает (убывает),
то существует обратная функция

, которая также строго возрастает (убывает).
Доказательство

Свойство симметрии графиков прямой и обратной функций

Пусть функция f(x) определена на некотором множестве X,
и имеет множество значений Y: f(X) ∈ Y.
И пусть она имеет на множестве X обратную функцию f^-1: f^-1(Y) ∈ X.
Тогда графики прямой

и обратной

функций, построенные при значениях их аргументов x ∈ X и x ∈ Y, соответственно, симметричны относительно прямой

.
Доказательство

Теорема о существовании и непрерывности обратной функции на отрезке

Пусть функция

непрерывна
и строго возрастает (строго убывает) на отрезке

.
Тогда на отрезке

определена и непрерывна обратная функция

, которая строго возрастает (строго убывает).
Для возрастающей функции

.
Для убывающей:

.
Доказательство

Теорема о существовании и непрерывности обратной функции на интервале

Пусть функция

непрерывна
и строго возрастает (строго убывает) на открытом конечном или бесконечном интервале

.
Тогда на интервале

определена и непрерывна обратная функция

, которая строго возрастает (строго убывает).
Для возрастающей функции

.
Для убывающей:

.
Доказательство

Теорема о существовании и непрерывности обратной функции на полуинтервале

Пусть функция

непрерывна и строго монотонна на полуинтервале X.
Тогда на полуинтервале Y определена, строго монотонна и непрерывна обратная функция

.
Если

строго возрастает, то

также строго возрастает. При этом:
если

, то

;
если

, то

.
Если

строго убывает, то

также строго убывает. При этом:
если

, то

;
если

, то

.
Здесь

. Открытый конец интервала может быть конечным числом или бесконечно удаленной точкой.
Доказательство

Примеры обратных функций

Арксинус

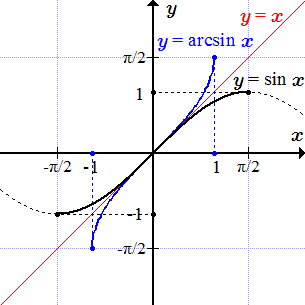
Графики sin(x) и arcsin(x) — Графики y = sin x и обратной функции y = arcsin x.

Рассмотрим тригонометрическую функцию синус: . Она определена и непрерывна для всех значений аргумента , но не является монотонной. Однако, если сузить область определения, то можно выделить монотонные участки. Так, на отрезке , функция определена, непрерывна, строго возрастает и принимает значения от –1 до +1. Поэтому имеет на нем обратную функцию, которую называют арксинусом. Арксинус имеет область определения и множество значений .

Логарифм

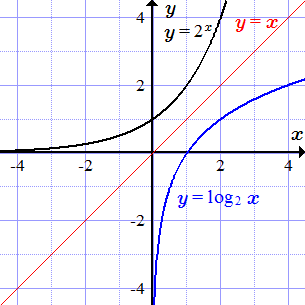
Показательная функция определена, непрерывна и строго возрастает при всех значений аргумента . Множеством ее значений является открытый интервал . Обратной функцией является логарифм по основанию два. Он имеет область определения и множество значений .

Квадратный корень

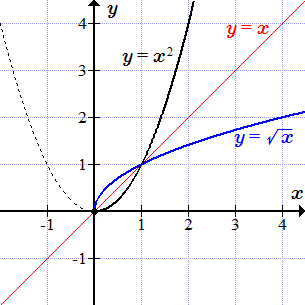
Графики x в квадрате и корень из x — Графики y = x² и обратной функции y = √x.

Степенная функция определена и непрерывна для всех . Множеством ее значений является полуинтервал . Но она не является монотонной при всех значений аргумента. Однако, на полуинтервале она непрерывна и строго монотонно возрастает. Поэтому если, в качестве области определения, взять множество , то существует обратная функция, которая называется квадратным корнем. Обратная функция имеет область определения и множество значений .

См. также: Примеры графиков обратных функций

Пример. Доказательство существования и единственности корня степени n

Все примеры Докажите, что уравнение , где n – натуральное, – действительное неотрицательное число, имеет единственное решение на множестве действительных чисел, . Это решение называется корнем степени n из числа a. То есть нужно показать, что любое неотрицательное число имеет единственный корень степени n.

Решение

Рассмотрим функцию от переменной x:
(П1) .

Докажем, что она непрерывна.
Используя определение непрерывности, покажем, что
.
Применяем формулу бинома Ньютона:
(П2)
.
Применим арифметические свойства пределов функции. Поскольку , то отлично от нуля только первое слагаемое:
.
Непрерывность доказана.

Докажем, что функция (П1) строго возрастает при .
Возьмем произвольные числа , связанные неравенствами:
, , .
Нам нужно показать, что . Введем переменные . Тогда . Поскольку , то из (П2) видно, что . Или
.
Строгое возрастание доказано.

Найдем множество значений функции при .
В точке , .
Найдем предел .
Для этого применим неравенство Бернулли. При имеем:
.
Поскольку , то и .
Применяя свойство неравенств бесконечно больших функций находим, что .
Таким образом, , .

Согласно теореме об обратной функции, на интервале определена и непрерывна обратная функция . То есть для любого существует единственное , удовлетворяющее уравнению . Поскольку у нас , то это означает, что для любого , уравнение имеет единственное решение, которое называют корнем степени n из числа x:
.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов. Опубликовано: 27-10-2018 Изменено: 16-02-2021

См. также: