Вывод производных обратных тригонометрических функций
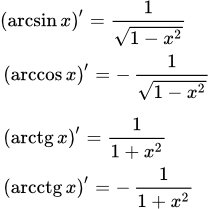
Вывод производных арксинуса и арккосинуса
Сначала выведем формулу производной арксинуса. Пусть
y = arcsin x.
Поскольку арксинус есть функция, обратная к синусу, то
sin y = x; – π2 ≤ y ≤ π2.
Здесь y – функция от x. Дифференцируем по переменной x:
(sin y) ′ = (x) ′ = 1.
Применяем формулу производной сложной функции:
(sin y) ′ = d sin ydx = d sin ydy ⋅ dydx = cos y ⋅ y ′.
Итак, мы нашли:
cos y ⋅ y ′ = 1.
Поскольку – π2 ≤ y ≤ π2, то cos y ≥ 0. Тогда
cos y = | cos y | = √ cos 2 y = √ 1 – sin 2 y = √ 1 – x 2 .
И предыдущая формула принимает вид:
√ 1 – x 2 ⋅ y ′ = 1. Отсюда
y ′ = (arcsin x) ′ = 1√ 1 – x 2 .
Точно таким способом можно получить формулу производной арккосинуса. Однако проще воспользоваться формулой, связывающей обратные тригонометрические функции:
arccos x = π2 – arcsin x.
Тогда
(arccos x) ′ = ( π2 – arcsin x ) ′ = – 1√ 1 – x 2 .
Более подробно изложение представлено на странице “Вывод производных арксинуса и арккосинуса”. Там дается вывод производных двумя способами – рассмотренным выше и по формуле производной обратной функции.
Вывод производных арктангенса и арккотангенса
Таким же способом найдем производные арктангенса и арккотангенса.
Пусть
y = arctg x.
Арктангенс есть функция, обратная к тангенсу:
tg y = x; – π2 < y < π2.
Дифференцируем по переменной x:
(tg y) ′ = (x) ′ = 1.
Применяем формулу производной сложной функции:
(tg y) ′ = d tg ydx = d tg ydy ⋅ dydx = 1cos 2 y ⋅ y ′.
Итак, мы нашли:
1cos 2 y ⋅ y ′ = 1.
Далее выразим 1cos 2 y через tg y и учтем, что tg y = x.
1cos 2 y = cos 2 y + sin 2 ycos 2 y = 1 + tg 2 y = 1 + x 2.
Тогда
( 1 + x 2 ) ⋅ y ′ = 1.
Отсюда
y ′ = (arctg x) ′ = 11 + x 2.
Производная арккотангенса:
(arcctg x) ′ = ( π2 – arctg x ) ′ = – 11 + x 2.
См. “Вывод производных арктангенса и арккотангенса”. На этой странице изложен вывод производных двумя способами – рассмотренным выше и по формуле производной обратной функции.
Производные высших порядков
Далее мы приводим некоторые соотношения и выражения для производных высших порядков от обратных тригонометрических функций. Полное изложение вывода формул производных высших порядков представлено на страницах Вывод производных высших порядков арксинуса и арккосинуса и Вывод производных высших порядков арктангенса и арккотангенса.
Производные арксинуса
Пусть
y = arcsin x.
Производную первого порядка от арксинуса мы уже нашли:
y ′ = 1√ 1 – x 2 .
Дифференцируя, находим производную второго порядка:
y ′′ = ( ( 1 – x 2 ) –1 / 2 ) ′ = – 12 ( 1 – x 2 ) –3 / 2 ⋅ ( 1 – x 2 ) ′ = – 12 ⋅ (–2x) ⋅ 1(1 – x 2) 3 / 2;
y ′′ = x(1 – x 2) √ 1 – x 2 .
Ее также можно записать в следующем виде:
y ′′ = x1 – x 2 y ′.
Отсюда получаем дифференциальное уравнение, которому удовлетворяют производные арксинуса первого и второго порядков:
( 1 – x 2 )y ′′ – xy ′ = 0.
Дифференцируя это уравнение, можно найти производные высших порядков.
Производная арксинуса n-го порядка
Производная арксинуса n-го порядка имеет следующий вид:
(arcsin x) (n) = pn (x)( 1 – x 2 ) 1 – 2n2,
где pn (x) – многочлен степени n – 1. Он определяется по формулам:
p2m + 1 (x) = A [1 + mΣk = 1 (m!) 2(2k)!( (m – k)! ) 2 (2x) 2k];
p2m (x) = Ax [1 + m – 1Σk = 1 ((m – 1)!) 2(2k + 1)!( (m – k – 1)! ) 2 (2x) 2k].
Здесь A = [1 ⋅ 3 ⋅ 5⋅ ⋅ ⋅(2m – 1)] 2 ≡ [(2m – 1)!!] 2.
Многочлен pn (x) удовлетворяет дифференциальному уравнению:
(1 – x 2) p ′′n(x) + (2n – 3) x p ′n(x) – (n – 1) 2 pn (x) = 0.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Производная арккосинуса n-го порядка
Производные для арккосинуса получаются из производных для арксинуса с помощью тригонометрической формулы:
arccos x = π2 – arcsin x.
Поэтому производные этих функций отличаются только знаком:
(arccos x) (n) = –(arcsin x) (n).
Производные арктангенса
Пусть y = arctg x. Мы нашли производную арккотангенса первого порядка:
y ′ = 11 + x 2.
Разложим дробь на простейшие:
11 + x 2 = 1(x – i)(x + i) = 12i x + i – (x – i)(x – i)(x + i) = 12i ( 1x – i – 1x + i ) =
i2 ( 1x + i – 1x – i ).
Здесь i – мнимая единица, i 2 = –1.
Дифференцируем n – 1 раз и приводим дробь к общему знаменателю:
y (n) = (–1) n – 1 (n – 1)! i2 ( 1(x + i) n – 1(x – i) n ) =
(–1) n – 1 i (n – 1)! ⋅ (x – i) n – (x + i) n2(1 + x 2) n.
Подставляя x = tg y, получим:
y (n) = (n – 1)! cos n y ⋅ sin[ n( y + π2 ) ].
Производная арктангенса n-го порядка
Таким образом, производную арктангенса n-го порядка можно представить несколькими способами:
y (n) = (–1) n – 1 i (n – 1)! ⋅ (x – i) n – (x + i) n2(1 + x 2) n;
y (n) = (n – 1)! cos n y ⋅ sin[ n( y + π2 ) ].
См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Производные арккотангенса
Пусть теперь y = arcctg x. Применим формулу, связывающей обратные тригонометрические функции:
arcctg x = π2 – arctg x.
Тогда производная n-го порядка от арккотангенса отличаются только знаком от производной арктангенса:
y (n) = –(arctg x) (n) = (–1) n i (n – 1)! ⋅ (x – i) n – (x + i) n2(1 + x 2) n.
Подставив x = ctg y, найдем:
y (n) = (n – 1)! sin n y ⋅ sin[ n( y + π ) ].
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: