Доказательство непрерывности тригонометрических функций
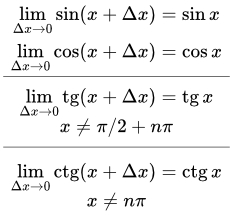
Формулировки лемм и теорем
выполняется неравенство:
(1.1) |sin α| ≤ |α|.
Здесь α – угол, выраженный в радианах.
Доказательство
непрерывны на своих областях определения.
Доказательство
Тригонометрические функции периодичны. Поэтому для определения обратных функций, используют интервалы, на которых они монотонны и непрерывны. Это можно сделать бесконечным числом способов. Поэтому выбирают интервалы, наиболее близко расположенные к нулевым положительным значениям. Полученные таким способом обратные тригонометрические функции называют главными значениями. См. «Определение обратных тригонометрических функций и их графики». Они имеют следующие области определения и множества значений:
(строго возрастает);
(строго убывает);
(строго возрастает);
(строго убывает).
непрерывны на своих областях определения.
Доказательство
Доказательство лемм и теорем
Лемма 1
Все свойства Для всех действительных чиселвыполняется неравенство:
(1.1) |sin α| ≤ |α|.
Здесь α – угол, выраженный в радианах.
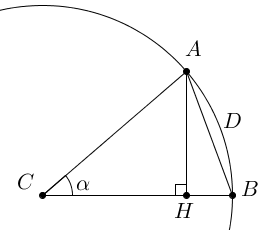
Рассмотрим случай .
Пусть точки A и B лежат на окружности с центром в точке C (см. рисунок). Тогда угол α между сторонами AC и BC есть отношение длины дуги окружности к радиусу :
.
Из точки A опустим перпендикуляр AH на BC. Тогда
.
Для упрощения расчетов мы возьмем окружность с радиусом, равным единице: . Тогда
(1.2) .
Из прямоугольника ABH имеем:
.
Поскольку длина отрезка |AB| является кратчайшим расстоянием между точками A и B, то
.
Из двух последних неравенств,
(1.3) .
Подставляем (1.2):
.
Знак равенства получается только при .
При отрицательных значениях ,
.
Эти выражения справедливы и для положительных значений . Подставляя в (1.3), при имеем:
.
Поскольку и , то это неравенство справедливо для всех α.
Лемма доказана.
Доказательство для синуса.
Используем неравенство (1.1):
(1.1) .
Перепишем его в следующем виде:
.
Заметим, что и . Применяя теорему о промежуточной функции, получаем:
.
Доказательство для косинуса.
При достаточно малых |α|, . Поэтому
.
Функция определена и непрерывна для всех x (см. Непрерывность и свойства степенной функции, Свойства степенных функций с различными значениями показателя степени). Тогда по теореме о пределе непрерывной функции от функции, имеющей предел, имеем:
.
Применим арифметические свойства непрерывных функций:
.
Степенная функция определена и непрерывна при . В частности, она непрерывна в точке . Применяя вышеупомянутую теорему о пределе непрерывной функции от функции, имеем:
.
Лемма доказана.
Теорема о непрерывности тригонометрических функций
Все свойства Тригонометрические функции: синус (sin x), косинус (cos x), тангенс (tg x) и котангенс (ctg x),непрерывны на своих областях определения.
Непрерывность синуса и косинуса
См. также «Синус и косинус – свойства, графики, формулы»
Применим определение непрерывности функции в терминах приращений. Нам нужно показать, что
.
Применим арифметические свойства предела функции, пределы, вычисленные в лемме 2 ⇑, и тригонометрические формулы:
.
Аналогично для косинуса:
.
Непрерывность тангенса и котангенса
См. также «Тангенс и котангенс – свойства, графики, формулы»
Тангенс и котангенс выражаются через синус и косинус:
.
Воспользуемся арифметическими свойствами непрерывных функций. Поскольку синус и косинус определены и непрерывны для всех x, то тангенс и котангенс определены и непрерывны для всех x, кроме точек, в которых знаменатель обращается в нуль:
;
.
Здесь n = 0, ±1, ±2, ±3, ... – целое число.
Теорема доказана.
Теорема о непрерывности обратных тригонометрических функций
Все свойства Обратные тригонометрические функции: арксинус (arcsin x), арккосинус (arccos x), арктангенс (arctg x) и арккотангенс (arcctg x),непрерывны на своих областях определения.
См. также «Обратные тригонометрические функции, их графики и формулы»
Непрерывность арксинуса
Функция синус, , строго возрастает при , где n – целое число. Она строго убывает при . Для определения главного значения обратной функции, берут наиболее близкий к нулю интервал, на котором синус является строго монотонной функцией. Это закрытый интервал с :
.
На нем функция синус непрерывна, строго возрастает и имеет множество значений
.
Тогда, по теореме о существовании и непрерывности обратной функции, на отрезке определена и непрерывна обратная функция, которая называется арксинусом (точнее главным значением арксинуса). Арксинус имеет множество значений .
Непрерывность арккосинуса
Функция косинус, , строго убывает при . Она строго возрастает при . Наиболее близким к нулю интервалом, на котором косинус является строго монотонной функцией, выбирают отрезок с положительными значениями:
.
На нем функция косинус непрерывна, строго убывает и имеет множество значений
.
По теореме о существовании и непрерывности обратной функции, на отрезке определена и непрерывна обратная функция, которая называется арккосинусом (точнее главным значением арккосинуса). Арккосинус имеет множество значений .
Непрерывность арктангенса
Функция тангенс, , определена, непрерывна и строго возрастает на открытых интервалах . Для определения главного значения обратной функции, берут интервал
.
На нем функция тангенс непрерывна, строго возрастает и имеет множество значений
.
Тогда, по теореме о существовании и непрерывности обратной функции, на интервале определена и непрерывна обратная функция, которая называется арктангенсом (точнее главным значением арктангенса). Арктангенс имеет множество значений .
Непрерывность арккотангенса
Функция котангенс, , определена, непрерывна и строго убывает на открытых интервалах . Для определения главного значения обратной функции, берут интервал
.
На нем функция котангенс непрерывна, строго убывает и имеет множество значений
.
Тогда, по теореме о существовании и непрерывности обратной функции, на интервале определена и непрерывна обратная функция, которая называется арккотангенсом (точнее главным значением арккотангенса). Арккотангенс имеет множество значений .
Теорема доказана.
Автор: Олег Одинцов. Опубликовано:
